Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more.


Table of Contents Univariate Data Distributions Most common distributons Hypergeometric Distribution
See also: Binomial Distribution, relationship between distributions 

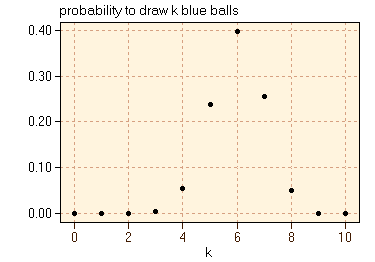
Hypergeometric Distribution


The hypergeometric distribution is a discrete distribution and is used to describe the probability to find k observations of class 1 when n objects are drawn from a population of N objects, and the probability of a single element of class 1 equals p.

Definition

N ... number of elements in population
n ... number of drawn samples
p ... probability of class 1
k ... observations of class 1

Graphical View
Applications Often used in quality control applications. 
First Moment m = np
Second Moment

Example

Suppose you have 20 balls in a bag, 8 blue ones, and 12 red ones. Now mix the balls in the bag and draw 15 balls. What is the probability to draw exactly 5 blue balls and 10 red balls? The answer to this question is given by the hypergeometric distribution function:

N = 20
n = 15
p = 0.4 (8 of 20 balls are blue)
k = 5

The probability to draw exactly 5 blue balls is 0.238 as can be seen from the following distribution curve:

Last Update: 2005-Dec-31