| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Multivariate Data Multivariate Data  Modeling Modeling  Classification and Discrimination Classification and Discrimination  LDA LDA  Linear Discriminant Analysis Linear Discriminant Analysis |
||||||||||
| See also: classification and discrimination, multiple linear regression - introduction | ||||||||||
Linear Discriminant Analysis - IntroductionLinear Discriminant Analysis (LDA) is a method to discriminate between
two or more groups of samples. In order to develop a classifier based on LDA, you have to perform the following steps:
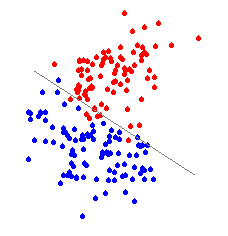 Definition of groups: The groups to be discriminated can be defined either naturally by the
problem under investigation, or by some preceding analysis, such as a cluster analysis. The number of groups is not restricted to two, although the
discrimination between two groups is the most common approach. Note that
the number of groups must not exceed the number of variables describing
the data set. Another prerequisite is that the groups have the same covariance
structure (i.e. they must be comparable).
Definition of discriminating function: In principle, any mathematical function may be used as a discriminating function. In case of the LDA, a linear function of the form y = a0 + a1x1 + a2x2 + ..... + anxn is used, with xi being the variables describing the data set. The parameters aihave to be determined in such a way that the discrimination between the groups is best. Note that this linear discriminating function is formally equivalent to the multiple linear regression. In fact, one can directly use MLR if the response variable y is replaced by the weighted class numbers c1 and c2: c1 = n2/(n1+n2) and c2 = - n1/(n1+n2) In order to get a better understanding of the working of the discriminating
function, start the following interactive example .
Estimation of the parameters of the discriminating function: As you have seen in the interactive example above, there is only one
direction of the discriminating line which yields the best separation results.
The determination of the coefficients of the discriminating function is
quite simple. In principle, the discriminating function is formed in such
a way that the separation (=distance) between the groups is maximized,
and the distance within the groups is minimized.
Test of the discriminating function When the discriminating function is parametrized, it has to be tested
either by using an independent set of test data, or by performing cross-validation.
In both cases, the results of the test set should be comparable to the
training data.
Application Discriminant analysis can be used to perform either analysis or classification:
|
||||||||||
Home  Multivariate Data Multivariate Data  Modeling Modeling  Classification and Discrimination Classification and Discrimination  LDA LDA  Linear Discriminant Analysis Linear Discriminant Analysis |
||||||||||

