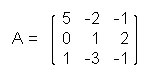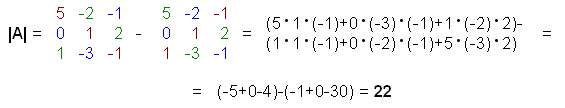| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Math Background Math Background  Matrices Matrices  Determinant Determinant  Matrix Determinants - Calculation of Order 2 and 3 Matrix Determinants - Calculation of Order 2 and 3 |
||||||||||
| See also: matrix determinant, rank of a matrix | ||||||||||
Matrix Determinants - Calculation of Order 2 and 3The general approach how to calculate a matrix determinant is hard, requiring the calculation of many similar steps. Thus it is not recommended to calculate a determinant of matrices with an order higher than 3 without the help of a computer. For matrices of order 2 and 3 there are special rules which make it comparatively easy to determine the determinant: Determinant of matrices of order 2 Let
be an arbitrary matrix of order 2. Then its determinant is calculated
as the product of the principal diagonal minus the product of the other
diagonal, formally a11 Determinant of matrices of order 3 (Sarrus' Rule) Let
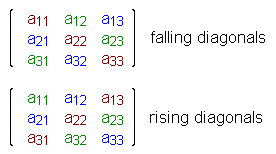
be an arbitrary matrix of order 3. Then its determinant is calculated
as the sum of the product of all "extended" falling (including the principal)
diagonals minus the sum of the product of all "extended" rising diagonals,
formally (a11
Example: determinant of a matrix of order 3 Let
Then
Please note that the rectangular, colored
schemes do not denote actual matrices, but are only included to emphasize the
rule of Sarrus.
|
||||||||||
Home  Math Background Math Background  Matrices Matrices  Determinant Determinant  Matrix Determinants - Calculation of Order 2 and 3 Matrix Determinants - Calculation of Order 2 and 3 |
||||||||||