| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Math Background Math Background  Matrices Matrices  Eigenvectors and Eigenvalues - Advanced Discussion Eigenvectors and Eigenvalues - Advanced Discussion |
|||||
| See also: linear equations, definition of eigenvalues and eigenvectors, The NIPALS Algorithm | |||||
Eigenvectors and Eigenvalues - Advanced DiscussionThe following section gives some hints on how eigenvectors can be calculated. In order to solve the fundamental equation A for its eigenvectors e and eigenvalues λ, we have to rearrange this equation (I is the identity matrix): A A (A -λ Note that from the last equation we cannot conclude that any of the product terms are zero. However, if we look at the determinants of this equation, |A -λ we see that a non-trivial solution is that |A -λ
Example: Characteristic Determinant
Finally, eigenvectors and eigenvalues are defined as a solution of the
characteristic function:
|
|||||
Home  Math Background Math Background  Matrices Matrices  Eigenvectors and Eigenvalues - Advanced Discussion Eigenvectors and Eigenvalues - Advanced Discussion |
|||||


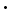 e
=λ
e
=λ