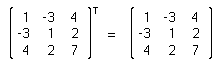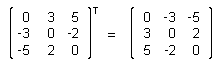Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more.

Home Math Background Matrices Transposed Matrix
See also: Inversion of a Matrix 
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter

Transposed Matrix


 
Transposed Matrix The transpose of a given matrix M of order mn is the matrix MT, which is obtained by exchanging the order of the indices: (mrs )T = (msr ). This new matrix MT is of the order nm.

More simply expressed, we just write the rows as columns, and vice versa. Here is an example:

 
It is evident that MTT equals M, where MTT is the transpose of the transpose of M.
 
 
Symmetric Matrix The matrix M is called symmetric if M = MT.
Skew-Symmetric Matrix If M = -MT, the matrix is called skew-symmetric or anti-symmetric.
Home Math Background Matrices Transposed Matrix

Last Update: 2010-03-18