Noise Addition
Generalization is a very important aspect when setting up non-linear
models (especially when using neural networks). In order to create well-performing
models, one has to check the generalization ability of the model. In this
respect, generalization can be seen as noise-immunity: the model should
not adapt itself to any noise present in the system. This aspect leads
us to the idea that the generalization behavior of a model can be tested
by adding increasingly more noise to the training data and checking the
stability of the model  . .
In order to perform the generalization test, we need two measures:
-
The goodness of fit of the estimation (square of correlation coefficient
between sample and estimated data): r2t,e
-
The square of the correlation coefficient between the estimated data of
the original data set and the estimated data calculated from the noisy
data: r2e0,en
These figures are calculated at various levels of noise. The trends
of these two figures as noise increases indicate the generalisation of
the network. A network which performs well will show a decreasing r2t,e,
since the increasing noise level will not be reflected in the estimated
function. On the other hand, the value of r2e0,en
should stay almost constant, since the estimated function of a noisy data
set will not differ much from the estimated function of the original data
set. The situation is just a mirror image when overfitting occurs: the
parameter r2t,e will be almost constant and
the value of r2e0,en will decrease with increasing
noise, since the networks tend to adjust themselves to the noisy sample
data, neglecting the underlying trend of the data.
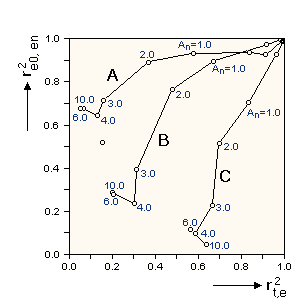 In the figure above, the dependence of r2t,e
and r2e0,en on various levels of added noise An
is shown for three networks of different size and generalization capability.
Curve A (good generalization): 400 data points, 15 hidden neurons, curve
B (medium generalization): 200 data points, 38 hidden neurons, curve C
(poor generalization): 100 data points, 70 hidden neurons.
In the figure above, the dependence of r2t,e
and r2e0,en on various levels of added noise An
is shown for three networks of different size and generalization capability.
Curve A (good generalization): 400 data points, 15 hidden neurons, curve
B (medium generalization): 200 data points, 38 hidden neurons, curve C
(poor generalization): 100 data points, 70 hidden neurons.
|


 Multivariate Data
Multivariate Data  Modeling
Modeling  Validation of Models
Validation of Models  Noise Addition
Noise Addition
 Multivariate Data
Multivariate Data  Modeling
Modeling  Validation of Models
Validation of Models  Noise Addition
Noise Addition
