| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  General Processing Steps General Processing Steps  Data Acquisition Data Acquisition  Analog/Digital Conversion Analog/Digital Conversion |
|||||
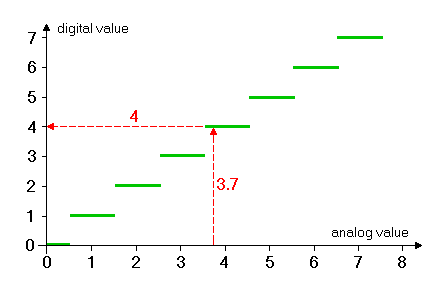
Analog/Digital ConversionLooking at the analog-digital conversion from an abstract point of view one can see that the process of digitization is nothing else but the application of a staircase function to the input signal. This way an exactly defined discrete value is assigned to each measured (analog) value.
The total number of steps N of the staircase function depends on the resolution k of the AD converter: N = 2k This means that, for example, an AD converter with 8 bit resolution maps the input signal to a total of 256 (28) steps, while a 12-bit AD converter maps its input range to 4096 steps. For a typical input voltage range of 10 volts (-5V to +5V) a single step of an 8-bit converter corresponds to approx. 40 mV, while a 12-bit converter shows a step size of 2.5 mV.Thus the AD conversion results in samples of the input signal at specific moments. However, the momentary amplitude of the signal is measured only within the limits of the resolution of the converter, and it is measured only at discrete time intervals, resulting in an error which is commonly called quantization noise. This quantization noise is the difference between the actual and the digitized signal and will decrease with increasing converter resolution k and increasing sampling frequency f=1/ts. As our ears are quite sensible to the quantization noise high fidelity audio equipment uses resolutions of 18 bits and higher.
Due to technical limits the resolution of the AD converters cannot be increased to arbitrary levels. Further, the costs for an AD converter approximately doubles with each additional bit, and the conversion speed decreases with higher resolutions. Thus each application of an AD converter always requires a compromise. Typical resolutions are 12 bits for cheap digital multimeters (31/2 digits), 12 to 16 bits for data acquisition equipment, and 16 to 20 bits for audio applications and high end measurement devices.
|
|||||
Home  General Processing Steps General Processing Steps  Data Acquisition Data Acquisition  Analog/Digital Conversion Analog/Digital Conversion |
|||||