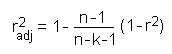Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more.

Home Multivariate Data Modeling Multiple Regression Coefficient of Determination and MLR
See also: Coefficient of Determination 

Coefficient of Determination and MLR

The coefficient of determination (goodness of fit) r2 of a multi-linear model can be calculated from the correlation coefficient between measured and estimated values. It indicates how well the model equation fits the data.

However, the goodness of fit depends not only on the quality of fit buut also on the number of observations and the number of variables. The goodness of fit can be deliberately brought towards 1.0 simply by including an increasing number of variables (descriptors) into the model equation.

In order to account for this fact you can either use the F-statistic obtained by the ANOVA of the model, or use an adjusted goodness of fit r2adj:

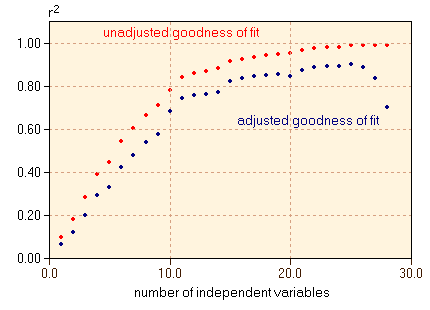
with n = number of observations, and k = number of variables.

The following figure shows the effects of adjusting the goodness of fit. A data matrix of 30 observations and 28 descriptors has been filled with random numbers. Calculating MLR models with an increasing number of variables increases the unadjusted goodness of fit towards 1.0 while the adjusted value decreases when the number of variables exceeds a certain limit.


Home Multivariate Data Modeling Multiple Regression Coefficient of Determination and MLR