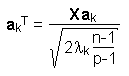| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Multivariate Data Multivariate Data  Modeling Modeling  PCA PCA  PCA of Transposed Matrices PCA of Transposed Matrices |
|||
| See also: Rank of a Matrix, PCA - Model Order | |||
PCA of Transposed MatricesIf we apply the principal component analysis to data matrices whose number of variables p is greater than the number of objects n (a classical example is the analysis of spectra when only a few samples are available), the calculation of the principal components may be quite time-consuming. This is due to the fact that the PCA is based on the solution of the eigenvalue problem for the covariance matrix. The dimension of the covariance matrix is p times p, which results in big matrices if p is large (i.e. if there are many variables).On the other hand we know from matrix algebra that the rank of a matrix cannot be greater than min(p,n) and, as a consequence, that the number of principal components is also limited to min(p,n). This means that for data sets with more variables than objects the number of calculations is unnessarily high as p - n principal components have to have zero eigenvalues. In order to speed up the calculation of the principal components we can transpose the data matrix before performing the principal component analysis. The covariance matrix of the transposed matrix is much smaller and thus faster to process. After the PCA has been applied to the transposed matrix, the results have to be transformed back according to the following equations:
with p .... number of variables of the original matrix λk .... eigenvalue of the k-th principal component of the original matrix λkT .... eigenvalue of the k-th principal component of the transposed matrix X .... original matrix ak .... k-th eigenvector of the original matrix akT .... k-th eigenvector of the transposed matrix
|
|||
Home  Multivariate Data Multivariate Data  Modeling Modeling  PCA PCA  PCA of Transposed Matrices PCA of Transposed Matrices |
|||