ANN - Backpropagation

Author: Hans Lohninger

Der erste Trainingsalgorithmus, der - historisch gesprochen - fähig war, mit verdeckten Schichten in neuronalen Netzwerken umzugehen, heißt "backpropagation of errors" (Fehlerrückleitung). Er wird zur Anpassung der Gewichte in einem mehrschichtigen Perzeptron (engl. multi-layer perceptron) verwendet, das eine Eingangsschicht, eine oder mehrere verdeckte Schichten und eine Ausgangsschicht hat. Mehrschichtige Perzeptrons werden oft auch als "Backpropagation-Netzwerke" bezeichnet, was den enormen Einfluss verdeutlicht, den dieser Algorithmus auf die Entwicklung künstlicher neuronaler Netzwerke hatte.

Die Grundprinzipien des Backpropagation-Algorithmus sind:

1. Der Fehler des Ausgangssignals eines Neurons wird verwendet, um seine Gewichtung so zu adjustieren, dass der Fehler verringert wird.
2. Der Fehler in versteckten Schichten wird proportional zur gewichteten Summe der (geschätzten) Fehler in der Schicht darüber gesetzt.

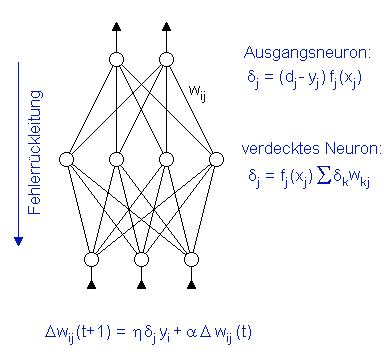
Während des Trainings werden die Daten dem Netzwerk einige tausend Male präsentiert. Für jede Datenprobe wird das Ausgangssignal des Netzwerks berechnet und dann mit dem "wahren" Sollwert verglichen. Das Fehlersignal δ_j des Neurons j wird von der Differenz zwischen dem Soll- und dem berechneten Ausgabewert berechnet. Für verdeckte Neuronen wird diese Differenz über die gewichteten Fehlersignale der darüber liegenden Schicht berechnet. Die Fehler werden dann verwendet, um die Gewichte w_ij des neuronalen Netzwerks abzustimmen.

Das Netzwerk stellt seine Gewichte nach jedem präsentierten Datensatz neu ein. Dieser Lernprozess entspricht eigentlich einem Gradientenabstieg in der Fehlerfläche des Gewichteraums - mit all seinen Nachteilen. Der Lernalgorithmus ist langsam und neigt dazu, in lokalen Minima stecken zu bleiben.

Für den Backpropagation-Algorithmus müssen die Anfangsgewichte der Neuronen relativ klein sein. Sie können zum Beispiel zufällig aus einem kleinen Intervall um null gewählt werden. Während des Trainings werden sie dann langsam angeglichen. Mit kleinen Gewichten zu starten ist entscheidend, weil große Gewichte unbeweglich sind und nicht schnell genug geändert werden können.

Das folgende interaktive Beispiel zeigt, wie ein mehrschichtiges Perzeptron lernt, Daten zu modellieren.