Neuronale Netze und Extrapolation

Author: Hans Lohninger

Neuronale Netze weisen - im Vergleich zu linearen Approximationsmethoden - einen großen Nachteil auf: Sie können nicht extrapolieren. Das ist darauf zurückzuführen, dass ein neuronales Netzwerk fast jede beliebige Funktion durch Anpassung seiner Parameter an die vorgegebenen Trainingsdaten darstellen kann. Für Bereiche des Variablenraums, für die es keine Trainingsdaten gibt, ist das Ergebnis des neuronalen Netzwerks unzuverlässig.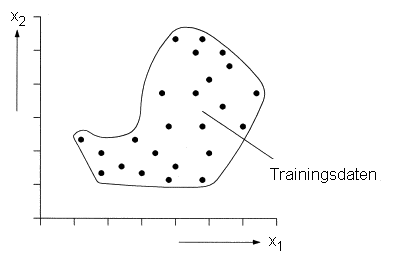

Grundsätzlich ist der Datenraum, der durch trainierte neuronale Netzwerke verarbeitet werden kann, in zwei Bereiche unterteilt:

1. Der Bereich, wo die Datendichte der Trainingsmenge größer als null ist und
2. alle anderen Teile des Datenraumes, wo die Dichte der Trainingsdaten null (oder beinahe null) ist.

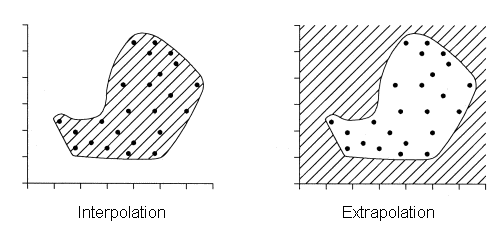
Um das Extrapolationsproblem kontrollieren zu können, sollte man den Umfang des Variablenraumes, in dem die Trainingsdaten verfügbar sind, in einer geeigneten Weise festhalten. Dies kann durch die Berechnung der konvexen Hülle der Trainingsdaten erfolgen. Wenn unbekannte Daten, die dem Netz vorgegeben werden, in dieser Hülle liegen, kann das Ergebnis des Netzes als verlässlich angesehen werden. Das Konzept der konvexen Hülle ist dennoch nicht zufriedenstellend, da diese Hülle schwer zu berechnen ist und keine Lösung für Probleme bietet, bei denen der Eingabedatenraum konkav ist. Eine bessere Methode, vorgeschlagen von Leonard et al. , besteht darin, die lokale Dichte der Trainingsdaten mit Hilfe eines Parzen-Fensters zu schätzen. Diese Methode ist auf alle Arten von Netzwerken anwendbar. RBF-Netzwerke bieten eine weitere, relativ einfache Methode zur Bestimmung von Extrapolationsbereichen .

Beispiel:

Das folgende Beispiel zeigt das Antwortverhalten neuronaler Netzwerke unter Extrapolationsbedingungen. Um die Erstellung des Netzwerkes zu vereinfachen, betrachten wir nur eindimensionale Eingabedaten, die im Zusammenhang mit einer einzelnen abhängigen Variablen stehen. Die Trainingsdaten sind im unteren Teil der nachfolgenden Grafik dargestellt. Die Anwendung von 15 trainierten Netzwerken auf die unbekannten Daten resultiert in Charakteristika, die in Bereichen mit verfügbaren Daten konsistent sind, während an anderen Stellen willkürliche Outputs produziert werden.