| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Neuronale Netze Neuronale Netze  RBF-Netzwerke RBF-Netzwerke  RBF-Netzwerke RBF-Netzwerke |
|
| Siehe auch: RBF-Netzwerk als Kernschätzer | |
| Search the VIAS Library | Index | |
|
RBF-NetzwerkeAuthor: Hans Lohninger
Radius-Basis-Funktions-Netzwerke (RBF-Netzwerke) stellen eine besondere Form
von neuronalen Netzwerken dar, die in engem Zusammenhang mit
Dichteschätzmethoden stehen. Einige, die sich mit diesem Thema beschäftigen,
bezeichnen es nicht als neuronales Netzwerk. Eine gründliche mathematische
Beschreibung von RBF-Netzwerken wird von Broomhead RBF-Netzwerke haben einen speziellen Aufbau, da sie nur aus drei Schichten (Eingabe, versteckte Schicht, Ausgabe) bestehen, und es nur eine Schicht gibt, in der die Neuronen ein nicht lineares Antwortverhalten zeigen. Einige Autoren schlugen vor, zusätzliche Neuronen einzubauen, die zur Berechnung der Verlässlichkeit des Ausgangssignals (Extrapolationsmarker) dienen.
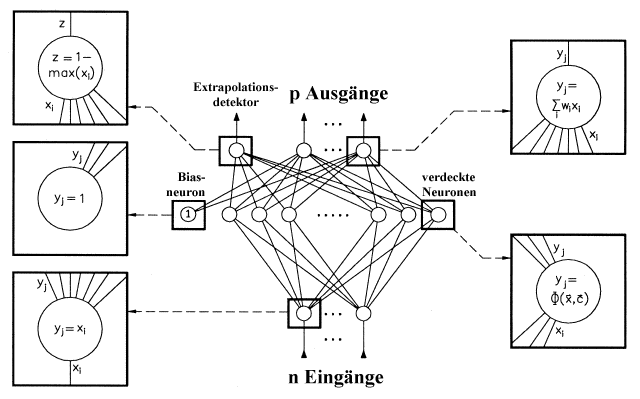 Die Eingangsschicht hat - wie in vielen anderen Netzwerkmodellen
auch - keine Rechenleistung, sondern dient nur dazu, die Eingabedaten auf die
versteckten Neuronen zu verteilen. Die versteckten Neuronen weisen eine nicht
lineare Transferfunktion auf, die sich von der Gauß'schen Glockenkurve ableitet.
Die Ausgabeneuronen wiederum haben eine lineare Transferfunktion, die es möglich
macht, auf sehr einfache Art und Weise die optimalen Gewichte zu berechnen.
|
|
Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Neuronale Netze Neuronale Netze  RBF-Netzwerke RBF-Netzwerke  RBF-Netzwerke RBF-Netzwerke |
|
Last Update: 2021-08-15

