| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Neuronale Netze Neuronale Netze  RBF-Netzwerke RBF-Netzwerke  RBF-Netzwerk als Kernschätzer RBF-Netzwerk als Kernschätzer |
|
| Siehe auch: RBF-Netzwerke | |
| Search the VIAS Library | Index | |
|
RBF-Netzwerk als KernschätzerAuthor: Hans Lohninger
RBF-Netzwerke gehören zur Klasse der Kernschätzermethoden. Diese Methoden benützen die gewichtete Summe einer endlichen Menge von nicht linearen Funktionen Φ(x-ci), um eine unbekannte Funktion f(x) anzunähern. Die Approximation wird aus den Datenproben, die dem Netzwerk vorgelegt werden, mit Hilfe folgender Gleichung aufgestellt: 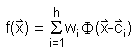 , ,Wobei h die Anzahl der Kernfunktionen ist, Φ() die Kernfunktion, x der Eingangsvektor, c ein Vektor, der das Zentrum der jeweiligen Kernfunktion im n-dimensionalen Raum repräsentiert, und wi sind die Koeffizienten, um die Näherungsfunktion f(x) anzupassen. Wenn diese Kernfunktionen in einen neuronalen Netzwerkaufbau eingebracht werden, kann ein dreischichtiges Netzwerk konstruiert werden, in dem jeder versteckte Knoten durch eine einzelne Kernfunktion repräsentiert wird und die Koeffizienten wi die Gewichte der Ausgabeschicht darstellen. Die Art jeder Kernfunktion kann aus einer großen Klasse von Funktionen
ausgewählt werden; wobei erst kürzlich bewiesen wurde, dass eine beliebige
Nicht-Linearität zur Darstellung jedes funktionellen Zusammenhangs durch das
Netzwerk ausreicht. Gauß'sche Kernfunktionen sind in der Literatur weit
verbreitet. Außerdem hat sich gezeigt, dass eine kleine Modifikation der
Gauß'schen Kernfunktion die Leistung des RBF-Netzwerks bei
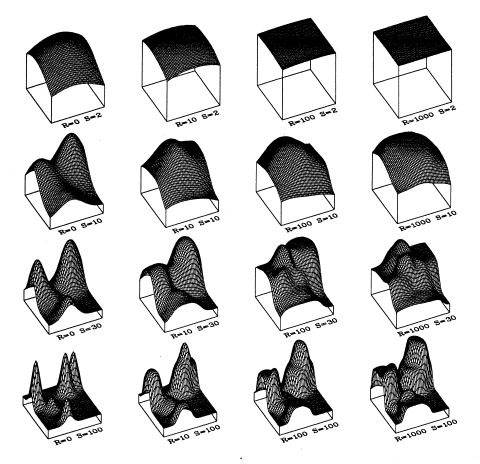
Klassifikationsaufgaben verbessert: 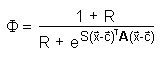 Wenn R den Wert null hat, ist die Kernfunktion eine klassische Gauß-Funktion (siehe nachfolgende Darstellung). Ein großes R schafft eine abgeflachte Spitze des Kerns, die sich mit steigendem R mehr und mehr einer Zylinderform annähert. 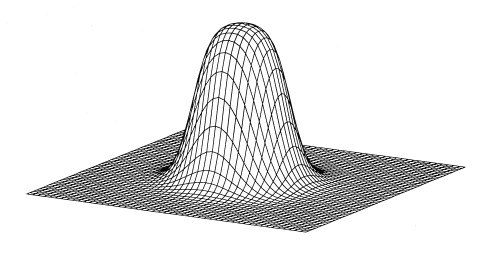 Die Ausgangsschicht eines RBF-Netzwerks kombiniert die Kernfunktion aller versteckten Neuronen mit einer linear gewichteten Summe dieser Funktionen. Abhängig von verschiedenen Parametern kann die Antwort des Netzwerks praktisch alle denkbaren Formen annehmen. Im Folgenden sind mehrere mögliche Response-Funktionen dargestellt, die man aus einem Netzwerk mit fünf versteckten Neuronen durch Variation der S- und R-Parameter erhält:
|
|
Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Neuronale Netze Neuronale Netze  RBF-Netzwerke RBF-Netzwerke  RBF-Netzwerk als Kernschätzer RBF-Netzwerk als Kernschätzer |
|
Last Update: 2021-08-15