| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Neuronale Netze Neuronale Netze  Rekursive Netzwerke Rekursive Netzwerke |
|
| Siehe auch: ANN - Einführung, Zeitreihen - Modelle von neuronalen Netzen | |
| Search the VIAS Library | Index | |
|
ANN - Rekursive NetzwerkeAuthor: Hans Lohninger
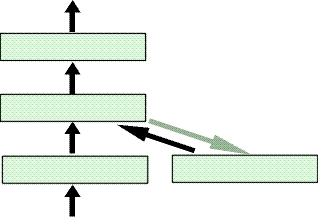
Netzwerke mit Feedbackschleifen gehören zur Gruppe der rekursiven Netzwerke. Bei diesen Netzwerken wird die Aktivierung der Neuronen nicht nur an die nächste Schicht weitergegeben, sondern auch an die Schicht davor, wodurch sich die Möglichkeit eines zyklischen Signalflusses ergibt. Zumindest theoretisch erlaubt das, eine unlimitierte Anzahl an vergangenen Aktivitäten in Berechnung des momentanen Signals mit einzubeziehen. Praktisch nimmt der Einfluss vergangener Eingangssignale jedoch rapide (exponentiell) ab. Die Geschwindigkeit der Abnahme kann zwar reguliert, aber nach ein paar Schritten die ursprüngliche Information nicht mehr erkannt werden. Rekursive Netzwerke sollten mit einem Trainingsalgorithmus trainiert werden, der den Fehler "rückwärts durch die Zeit" fortpflanzt. Diese Konsequenz ergibt sich aus einer Serie von vergangenen Eingaben, die einen Einfluss auf spätere Ausgaben haben. Man kann sich von dieser Technik ein Bild machen, indem man das Netzwerk mit dem Zeitfaktor darstellt [Hertz et al., 1991]. Diese Technik wird im BPTT-Algorithmus (Back Propagation Through Time) verwendet. Weil der Aufwand, den Fehler rückwärts durch die Zeit fortzupflanzen, sehr hoch ist, wird der zeitliche Aspekt während des Trainings oft ignoriert. Einfache rekursive NetzwerkeEin typisches Beispiel für einfache regressive Netzwerke ist das Elman-Netzwerk.
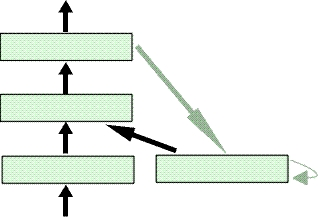
Ein anderes Beispiel für einfach rekursive Netzwerke ist
das Jordan-Netzwerk.
Das Zusammenlegen kann mittels Gewichtung und Addition der Aktivierung der Einheiten durchgeführt werden. Zum Beispiel kann die Aktivierung einer Einheit in der Erinnerungsschicht at die Ausgabe ot-1 folgenderweise beinhalten: at := 0.5 at-1 + 0.5 ot-1. Natürlich können diese Gewichte verändert werden. Die Erinnerungsschicht kann auch als Zustand des Netzwerks betrachtet werden. Überdies können verschiedenste Techniken zur Handhabung sequenzieller Informationen, wie zum Beispiel verschiedene Arten der Zeitverzögerung, Feedbackschleifen und Erinnerungsschichten, kombiniert werden, um noch stärkere temporale neuronale Netzwerke zu schaffen. Die Stärke solcher Netzwerke ist, dass sie Erinnerungen verschiedener Länge kombinieren. Doch große Netzwerke haben eine große Anzahl an Freiheitsgraden und das erschwert ihr Training. Vollständig rekursive NetzwerkeDas Fully Recurrent Network (FRN), das in Williams et al.
|
|
Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Neuronale Netze Neuronale Netze  Rekursive Netzwerke Rekursive Netzwerke |
|
Last Update: 2021-08-15