| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Grundlagen Grundlagen  Signale und Daten Signale und Daten  Faltung Faltung  Mathematische Details Mathematische Details |
|
| Siehe auch: Faltung - Einführung, Faltung - Rechenregeln | |
| Search the VIAS Library | Index | |
|
Faltung - Mathematische DetailsAuthor: Hans Lohninger
Das deutsche Wort für Konvolution, "Faltung", beschreibt den Vorgang treffend. Zwei Signale g(t) und h(t) werden durch Multiplizieren und Addieren der Produktterme gefaltet, wobei eines der Signale entlang der Zeitachse gespiegelt und verschoben wird. Das (diskrete) Faltungsergebnis für eine gegebene Verschiebung t ist definiert als
wobei 2n das Maximum der Probenanzahl von beiden Signalen ist. Die Summe der Produkte wird "diskrete Faltung" genannt. Im Fall kontinuierlicher Funktionen g(x) und h(x) wird aus der Produktsumme ein Integral:
Zum besseren Verständnis der Faltung kann man sich die Faltungsoperation als Gewichtung des Signals g(x) mit dem (gespiegelten) Signal h(x) vorstellen, wobei die Gewichtungsfunktion h(x) über den gesamten Definitionsbereich der Funktion g(x) verschoben wird und das Ergebnis als Funktion der Verschiebung t gesehen wird. Das folgende interaktive Beispiel ermöglicht es, mit unterschiedlichen Faltungsfunktionen zu experimentieren. Der Faltungsoperator weist wie andere Operatoren auch eine eigene Algebra auf, die wichtigsten Gesetze sind hier zusammengefasst.
|
|
Home  Grundlagen Grundlagen  Signale und Daten Signale und Daten  Faltung Faltung  Mathematische Details Mathematische Details |
|
Last Update: 2021-08-15


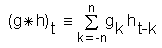 ,
,