| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Statistische Tests Statistische Tests  Grundlagen Grundlagen  Fehlerarten Fehlerarten |
|||||
| Siehe auch: Testen von Hypothesen, Trennschärfe eines Tests, Einseitige und zweiseitige Tests, Voraussetzung von statistischen Tests | |||||
| Search the VIAS Library | Index | |||||
|
FehlerartenAuthor: Hans Lohninger
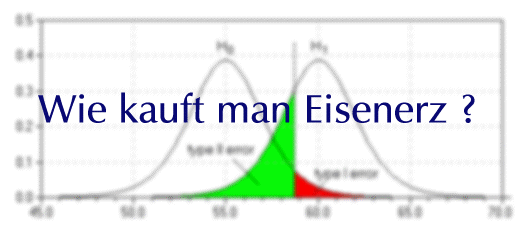
Es gibt zwei verschiedene Fehlerarten, die auftreten können, wenn eine Entscheidung getroffen wird: Fehler 1. Art treten auf, wenn wir die Nullhypothese verwerfen, obwohl sie wahr ist. Fehler der 2. Art treten auf, wenn wir die Nullhypothese nicht verwerfen, obwohl sie falsch ist (also die Alternativhypothese richtig ist).
Das folgende Beispiel soll helfen, die beiden Fehlerarten besser zu verstehen. Stellen Sie sich vor, Sie wollen Erz kaufen, um Eisen zu produzieren. Sie entscheiden, dass das Erz eine bestimmte minimale Konzentration von Eisen aufweisen muss, um für den Prozess verwendbar zu sein. Weil die Konzentration von Eisen bei jeder Lieferung schwankt, müssen Sie sicherstellen, dass das gelieferte Erz im Durchschnitt mehr als die spezifizierte minimale Konzentration enthält. Um vorsichtig zu sein, vertrauen Sie Ihren Lieferanten nicht. Zur Sicherheit nehmen Sie an, dass die Lieferanten Ihre Anforderungen nicht erfüllen können (H0 oder Nullhypothese). Sie glauben den Lieferanten nur dann, wenn sie Ihnen nachweisen können, dass Ihre Anforderungen erfüllt werden (H1 oder Alternativhypothese). Weil unsere Entscheidung richtig oder falsch sein kann und die Nullhypothese auch richtig oder falsch sein kann, gibt es vier mögliche Ergebnisse eines Tests. Die Wahrscheinlichkeiten für einen Fehler vom Typ 1 oder 2 werden normalerweise mit α bzw. β angegeben.
Im oben angegebenen Fall schädigt uns ein Fehler der 2. Art nicht, ausgenommen einer der abgewiesenen Anbieter bietet das Erz um einen sehr viel geringeren Preis an. Im Gegensatz dazu ist ein Fehler 1. Art für uns nachteilig, denn das würde bedeuten, dass wir das Erz kaufen, ohne den gewünschten Eisengehalt zu bekommen. Eine ausführlichere Beschreibung der Fehlerproblematik finden Sie im folgenden interaktiven Beispiel:
ANMERKUNGEN
|
|||||
Home  Statistische Tests Statistische Tests  Grundlagen Grundlagen  Fehlerarten Fehlerarten |
|||||
Last Update: 2014-04-28