| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Multiple Regression Multiple Regression  Maximum Likelihood Methode Maximum Likelihood Methode |
|
| Search the VIAS Library | Index | |
|
Maximum Likelihood MethodeAuthor: Hans Lohninger
Die Maximum Likelihood-Methode stellt eine Alternative zur Methode der kleinsten Quadrate dar. Der Begriff "Maximum Likelihood" wurde von R.A. Fisher 1922 geprägt und läuft auf die Aufgabe hinaus, eine sog. Likelihood-Funktion (oder deren Logarithmus) zu maximieren. Ganz allgemein kann man die Likelihood-Funktion L (welche die Wahrscheinlichkeit angibt, dass ein bestimmte Kombination von Werten der abhängigen Variablen Y auftritt), wie folgt definieren:
L = F(Y,Modell) = was bedeutet, dass die Wahrscheinlichkeiten des Auftretens der einzelnen (Mess-)Werte der abhängigen Variablen yi über den gesamten Datensatz multipliziert werden und damit die Wahrscheinlichkeit berechnet wird, genau diese Kombination an y-Werten zu bekommen, die in der Messung erzielt wurde (in der Praxis wird man statt des Produktes P, die Summe der Logarithmen der Wahrscheinlichkeiten bilden). Theoretisch könnten wir also die Wahrscheinlichkeit L, dass ein bestimmter Wert Y in unserer Stichprobe vorkommt, berechnen, falls wir die Modellparameter kennen. Da wir aber die Modellparameter nicht kennen (sondern, ganz im Gegenteil, erst finden müssen), müssen wir uns einen Weg ausdenken, diese abschätzen zu können. Dabei hilft uns folgende grundlegende Idee: Given the respective model, the larger the likelihood of the model, the larger is the probability of the dependent variable values to occur in the sample. Therefore, the greater the likelihood, the better is the fit of the model to the data. The actual computations for particular models here can become quite complicated because we need to "track" (compute) the probabilities of the y-values to occur (given the model and the respective x- values). As it turns out, if all assumptions for standard multiple regression are met (as described in the Multiple Regression chapter in the manual), then the standard least squares estimation method (see above) will yield results identical to the maximum likelihood method. If the assumption of equal error variances across the range of the x variable(s) is violated, then the weighted least squares method described earlier will yield maximum likelihood estimates.
|
|
Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Multiple Regression Multiple Regression  Maximum Likelihood Methode Maximum Likelihood Methode |
|
Last Update: 2013-04-01


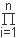 {p [yi, Modellparameter(xi)]},
{p [yi, Modellparameter(xi)]},