| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Multivariate Data Multivariate Data  Modeling Modeling  Neural Networks Neural Networks  RBF Neural Networks RBF Neural Networks  RBF Network as Kernel Estimator RBF Network as Kernel Estimator |
|
| See also: RBF network | |
RBF Network as Kernel EstimatorRBF neural networks belong to the class of kernel estimation methods. These methods use a weighted sum of a finite set of nonlinear functions Φ(x-ci) to approximate an unknown function f(x). The approximation is constructed from the data samples presented to the network using the following equation:
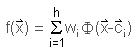 , ,
where h is the number of kernel functions, Φ() is the kernel function, x is the input vector, c is a vector which represents the center of the kernel function in the n-dimensional space, and wi are the coefficients to adapt the approximating function f(x). If these kernel functions are mapped to a neural-network architecture, a three-layered network can be constructed where each-hidden node is represented by a single kernel function and the coefficients wi represent the weights of the output-layer. The type of each kernel function can be chosen out of a large class of functions and in fact, it has been shown more recently that an arbitrary non-linearity is sufficient for representing any functional relationship by a neural network. Gaussian kernel functions are widely used throughout the literature. It has been shown that a small modification to the Gaussian kernel function improves the performance of RBF-networks for classification tasks:
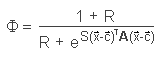
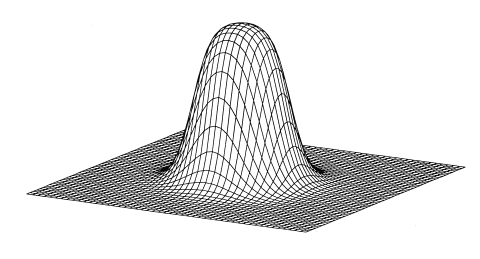
When R equals 0, the kernel function is the classical Gaussian function (see figure below). A large R creates a flat top of the kernel which more and more approaches the form of a cylinder with increasing R.
The output layer of an RBF network combines the kernel function of all hidden neurons with a linear-weighted sum of these functions. Depending on various parameters, the response of the network can assume virtually all thinkable shapes. Several possible response functions obtained from a network with five hidden neurons by varying the S and the R parameters are displayed below.
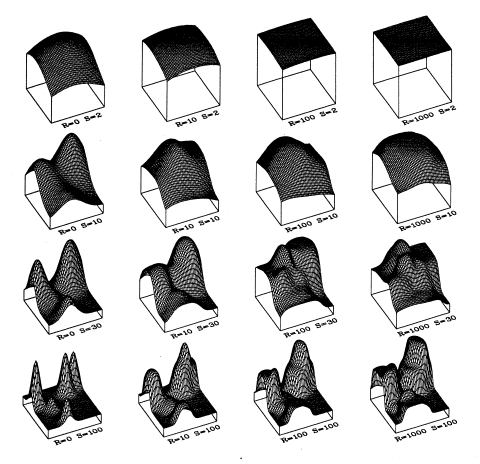
|
|
Home  Multivariate Data Multivariate Data  Modeling Modeling  Neural Networks Neural Networks  RBF Neural Networks RBF Neural Networks  RBF Network as Kernel Estimator RBF Network as Kernel Estimator |
|

