| Commutativity |
f g = g g = g f f
The order of the operands (functions) is exchangeable. |
| Associativity |
f (g (g h) = (f h) = (f g) g) h = f h = f g g h h
Convolution operations can be combined in arbitrary ways (the order in which the operations are performed does not matter). |
| Distributivity |
f (g+h) = f (g+h) = f g + f g + f h h
The distributive law corresponds to the distributive law of the arithmetic multiplication. |
| Scalar Multiplication |
a(f g) = (af) g) = (af) g = f g = f (ag) (ag)
If a function is multiplied by a scalar, the results of the convolution has to be multiplied by this scalar as well. |
| Convolution Theorem |
F (g h) = h) =  F (g) F (g)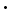 F (h) F (h)
The Fourier transform F() of a convolution product is proportional to the product of the Fourier transforms of the individual functions g and h. |
| Derivation Rule |
D(g h) = D(g) h) = D(g) h = g h = g D(h) D(h)
The first derivative D() of a convolution product is equal to the convolution of one of the original functions and the first derivative of the other function. Please note that for discrete sequences the first derivative is the difference between two consecutive elements of the sequence: D(gn) = gn+1 - gn |


 Basic Concepts
Basic Concepts  Signals and Data
Signals and Data  Convolution
Convolution  Calculation Rules
Calculation Rules Basic Concepts
Basic Concepts  Signals and Data
Signals and Data  Convolution
Convolution  Calculation Rules
Calculation Rules

 g = g
g = g F (g)
F (g)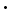 F (h)
F (h)