Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more.

Home Bivariate Data Correlation Distribution of the Correlation Coefficient
See also: correlation coefficient, random variable, chance correlation, testing the significance of r 
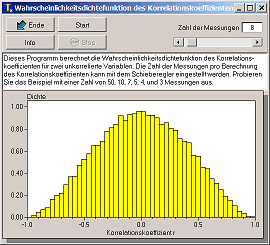
del.icio.us Reddit Facebook StumbleUpon MySpace Twitter

Distribution of the Correlation Coefficient

It should be noted that the correlation coefficient r is a random variable, thus having a distribution function which depends on the population value of the correlation coefficient ρand the number of samples n.

From the images above one can conclude that for a small number of observations it is quite likely that the correlation coefficient is high. A high correlation coefficient does not necessarily represent a high correlation between two variables. Especially with four sample values, any correlation coefficient is equally likely to occur. You may test this phenomenon yourself by starting the following  interactive example .

As a consequence of this effect, one has to test for the significance of a correlation coefficient.

Home Bivariate Data Correlation Distribution of the Correlation Coefficient

Last Update: 2010-12-17