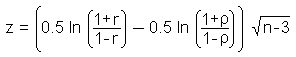| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Statistical Tests Statistical Tests  Correlation Coefficient Correlation Coefficient  Test: Correlation Coefficient Test: Correlation Coefficient |
|
| See also: survey on statistical tests, correlation coefficient, distribution calculator, distribution of the correlation coefficient | |
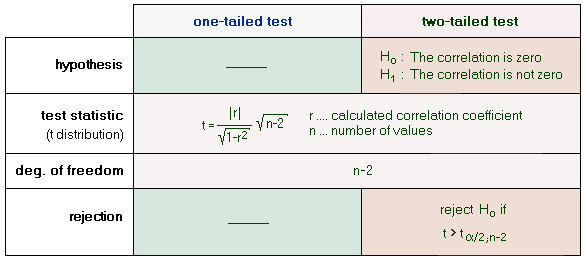
Test: Correlation Coefficient
A correlation coefficient of zero indicates that there is no linear relationship between two variables. In order to test the significance of a correlation coefficient we can use a test statistic t:  This test statistic is distributed according to a t-distribution. The correlation coefficient is considered to be statistically significant if the computed t value is greater than the critical value of a t-distribution with a level of significance of α/2 and n-2 degrees of freedom.
In order to test the hypothesis whether a calculated correlation coefficient r is different from the population coefficient ρ, we have to calculate the test statistic z which exhibits a standard normal distribution. r and ρare considered not to be from the same population if z is greater than the critical value of a standard normal distribution with a selected level of significance.
|
|
Home  Statistical Tests Statistical Tests  Correlation Coefficient Correlation Coefficient  Test: Correlation Coefficient Test: Correlation Coefficient |
|