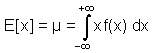| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Univariate Data Univariate Data  Distributions Distributions  Expectation Expectation |
|
| See also: algebra of expectation, random variable | |
ExpectationThe mathematical expectation is a concept which is often misunderstood and confused with the mean. In fact the expectation could be the mean, but must not necessarily be the same. The expectation is a more general concept which provides a formalism to estimate the expected value of a random variable (a function) for a population with a known probability distribution function. The expectation of a continuous random variable can be calculated as follows The corresponding equation for discrete random variables is
n .... number of observations
If the probabilities of all n observations p(
There are several rules concerning
expectation values which can be applied to derive the expected values
of more complicated random variables.
|
|
Home  Univariate Data Univariate Data  Distributions Distributions  Expectation Expectation |
|