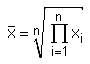Mean

The mean is commonly called the average. It is calculated by adding all the values and dividing the sum by the number of values. Let x_i represent the values of a variable X, with i = 1, 2, ..., n. The mean  is then defined as:

Note that there are also different definitions of the word mean (i.e. the geometric or the arithmetic mean). When the word "mean" is used without a modifier, it usually refers to the arithmetic mean as defined by the formula above.

Here is a simple  interactive example  for a "natural" computation of the mean.

Please note that there are different notations for the mean: the mean of a population is denoted by m, whereas the mean of the scores of a sample is denoted either by m, or by .

The mean is a good approximation of the central tendency for unimodal symmetric distributions, but can be misleading in skewed or multimodal distributions. Therefore, it can be useful to specify other additional measures of location for skewed distributions.

Hint 1:     It can be shown that the sum of squared deviations of sample scores from their mean is lower than the squared deviations from any other value.

Hint 2:    The mean is also often related to the accuracy of an experiment. See the following  interactive example  to get an impression of accuracy versus precision.