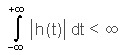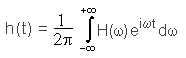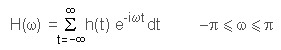Fourier Transformation
Introduction

The Fourier transformation provides the means to convert a signal from its representation in the time (as it is most often measured) to its representation in the frequency domain. The Fourier transform is reversible, making it possible to choose any representation for processing a signal. The Fourier transform is a generalization of the Fourier series to an infinite interval: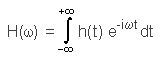

For transforming the signal back into the time domain the inverse Fourier transform can be applied:

Replacing the integral with a sum leads to the discrete Fourier transform (DFT), which can be applied to digitized data:

For practical situations the Fourier transform in its original form involves one major problem: it takes too many computational steps to be performed in real-time for many signals. Fortunately there is a family of equivalent algorithms which has been originally developed by Runge, and Danielson and Lanczos which is much faster than the original DFT algorithm. J.W. Cooley rediscovered this technique, which has been called "Fast Fourier Transform" (FFT) since then.