| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Bivariate Data Bivariate Data  Time Series Time Series  Fourier Transformation Fourier Transformation  Fourier Series Fourier Series |
|||||||||||||||
| See also: Fourier transformation, FFT | |||||||||||||||
Fourier SeriesAny periodic signal y(t) may be constructed from an infinite sum of sine and cosine terms:
with An and Bn being the Fourier coefficients, and T the cycle time of the function y(t). The coefficient A0 represents the aperiodic fraction of the signal (i.e. A0 is equal to the average amplitude of the signal). Alternatively, the signal y(t) may be described by the magnitudes Dn and the phase angles φn:
φn = tan-1 (Bn/An).
The index n in the equations above can be assigned to a specific frequency fn:
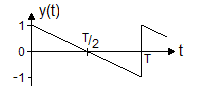
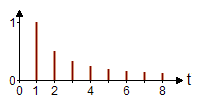
fn = n In practical settings one usually takes the magnitude and the phase angle to get the magnitude spectrum and the phase spectrum. If we plot the square of the magnitude against the frequency we get the power spectrum of the signal. Examples of Fourier seriesThe following table shows a few examples of simple periodic functions. The displayed magnitude spectra are normalized to a maximum value of 1.0 and ignore the actual signal amplitudes.
|
|||||||||||||||
Home  Bivariate Data Bivariate Data  Time Series Time Series  Fourier Transformation Fourier Transformation  Fourier Series Fourier Series |
|||||||||||||||



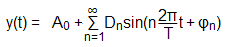

 f0
f0