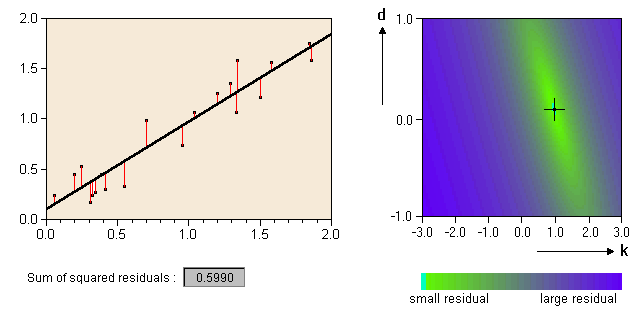
Optimization - Response Function

In order to optimize a given problem, one has to identify a response function which defines the relationship between the independent predictor variables and the "goal" of the optimization. The response function is sometimes also called the objective function, or quality function.

Many problems in statistical analysis can be redefined as a solution to an optimization problem. A simple example will show this: one has a set of two-dimensional data and there is the need to fit a straight line to the data. In more mathematical terms, the model can be described by

where y is the variable to be predicted by the model, and x represents the input data. K and d are the parameters to be found (=  to be optimized). We could therefore define a response function which calculates the sum of squared residuals. The best fit minimizes the response function. In the figure below, you see at the left side a straight line which fits the given data best, on the right side you see a representation of the phase space of the objective function. Click into the image to become more familiar with this concept.