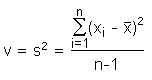Variance

In addition to the measures of location for describing the position of the distribution of a variable, one has to know the spread of the distribution (and, of course, about its form). Maybe you want to have a look at the following  interactive example  in order to see some examples of common means but different spreads.

The spread of a distribution may be described using various parameters, of which variance is the most common one. Mathematically speaking, the variance v is the sum of the squared deviations from the mean divided by the number of samples less 1:

• Why take the sum of squares and not, for example, the sum of absolute deviations from the mean? The answer to this is quite simple: the mathematical analysis is simpler, if the sum of squares is used.
• Why is the sum divided by n-1; wouldn't it be more logical to take just n? Here again, the answer is simple, but requires the introduction of the concept of the degree of freedom.
• What about the s² in the formula? The parameter s which is apparently the square root of the variance is called the standard deviation.

The variance of some data is closely related to the precision of a measuring process, as can be seen in the following  interactive example .