| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Math Background Math Background  Probability Probability  Additivity rule and mutually exclusive events Additivity rule and mutually exclusive events |
|||||
| See also: Summation of Probabilities | |||||
Additivity Rule
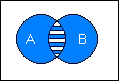
The most simple method to determine the probability of a union of events is to count the sample points of the compound set (provided that the individual probabilities are equal). Sample points which belong to both sets of the compound event are counted only once. If we naively tried to calculate the probability of the union by simply adding the probabilities of the original sets A and B, we would find that the sum of the probabilities of the sets A and B is greater than the probability of the union of A and B. The difference is given by the probability of the intersection of A and B. From these considerations the probability of the union of two events can be calculated as follows: P(A) + P (B) = P(A so the probability of the union of two events A and B is given by: 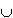 B) = P(A) + P (B) - P(A B) = P(A) + P (B) - P(A  B).
B).
Mutually exclusive events:Events A and B are mutually exclusive events,
if A P(A
|
|||||
Home  Math Background Math Background  Probability Probability  Additivity rule and mutually exclusive events Additivity rule and mutually exclusive events |
|||||