| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Math Background Math Background  Probability Probability  Calculating with Sets Calculating with Sets |
|||||||||||||||||||||||||||||||||||||||||||||||||
| See also: union, intersection, complement | |||||||||||||||||||||||||||||||||||||||||||||||||
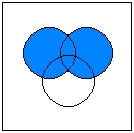
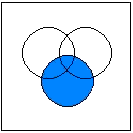
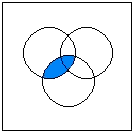
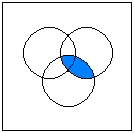
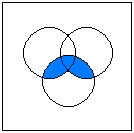
Calculating with SetsWhen combining two or more sets by union or intersection, the following rules
have to be applied:
A visualization of the distributive law:
|
|||||||||||||||||||||||||||||||||||||||||||||||||
Home  Math Background Math Background  Probability Probability  Calculating with Sets Calculating with Sets |
|||||||||||||||||||||||||||||||||||||||||||||||||


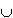 B = B
B = B  C =
C =