Complementary Sets and Subsets
| Complementary Set |
 The complementary event A' is the set of all elements which do not belong to it. It is often symbolized by A' or The complementary event A' is the set of all elements which do not belong to it. It is often symbolized by A' or  A. All sampling points of a population are either in A or in A', and no sample point can be a member of both A and A'. A. All sampling points of a population are either in A or in A', and no sample point can be a member of both A and A'. |
The sum of the probabilities of the event A and its complementary event A' is
one.
P(A) + P(A') = 1
In some cases, it is easier to calculate P(A') than to calculate P(A). In such cases we can obtain P(A) by P(A) = 1 - P(A').
| Example: |
When we toss a coin 5 times and define the event A as "at least one head", it is already a lot of work just to list all the possible outcomes. However, we can easily show that the total number of possible outcomes is 25=32. Thus the probability of each outcome is 1/32. The complementary event A' is no heads and consists only of one sample point: TTTTT. So we can calculate the probability of event A by P(A) = 1 - P(A') = 1- 1/32 = 0.96875. |
| Subsets |
 When the sample points of event A are a subset of the sample points of B, then A is said to be contained in B, and is written as A When the sample points of event A are a subset of the sample points of B, then A is said to be contained in B, and is written as A 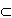 B. Thus, when A B. Thus, when A 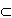 B, then the occurrence of A necessarily implies the occurrence of B. One can easily see that the probability P(A) is less than the probability P(B). B, then the occurrence of A necessarily implies the occurrence of B. One can easily see that the probability P(A) is less than the probability P(B). |
|


 Math Background
Math Background  Set Theorie
Set Theorie  Complementary Sets and Subsets
Complementary Sets and Subsets Math Background
Math Background  Set Theorie
Set Theorie  Complementary Sets and Subsets
Complementary Sets and Subsets

 The complementary event A' is the set of all elements which do not belong to it. It is often symbolized by A' or
The complementary event A' is the set of all elements which do not belong to it. It is often symbolized by A' or  A. All sampling points of a
A. All sampling points of a  When the sample points of event A are a subset of the sample points of B, then A is said to be contained in B, and is written as A
When the sample points of event A are a subset of the sample points of B, then A is said to be contained in B, and is written as A 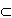 B. Thus, when A
B. Thus, when A