| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Math Background Math Background  Set Theorie Set Theorie  Union and Intersection Union and Intersection |
||||||||||||||||||||||||||||||||
| See also: Complementary Sets and Subsets | ||||||||||||||||||||||||||||||||
Union and Intersection
Compound events are formed from several sample points belonging to different events. These operations can be described by set theory
and its operators. These operations can be nicely visualized and easily understood by using the so-called Venn diagram. The most basic operators are the union and intersection.
Example: Let us take a quick look at the game Roulette (the European version with only one zero field): How many numbers let us win, if we bet on the red numbers and the numbers
of the third column? In order to evaluate this we have to
calculate the union of the set A (the red numbers) and the
set B (the numbers in the third column). A
How many numbers win twice if we bet on red and the third column? In order to win twice the selected number has to be an element of the intersection of set A (red numbers) and set B (numbers in the third column). The insection contains 8 numbers, thus we have a chance of 8/37 to win twice.
The probabilities of compound events can be calculated by counting the sample points and applying the summation rule. In addition, there exist some rules to calculate the probabilities for more complex problems which do not allow to count the sample points.
|
||||||||||||||||||||||||||||||||
Home  Math Background Math Background  Set Theorie Set Theorie  Union and Intersection Union and Intersection |
||||||||||||||||||||||||||||||||


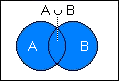 The union of the two sets A and B is defined as the set of all
events which belong either to set A or to set B. The union corresponds to
the logical OR and is denoted using the symbol
The union of the two sets A and B is defined as the set of all
events which belong either to set A or to set B. The union corresponds to
the logical OR and is denoted using the symbol 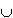
 The intersection of the two sets A and B is defined as the set of events which belong to both A and B. The intersection corresponds to the logical AND and is denoted using the symbol
The intersection of the two sets A and B is defined as the set of events which belong to both A and B. The intersection corresponds to the logical AND and is denoted using the symbol  .
.