| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Bivariate Data Bivariate Data  Time Series Time Series  Fourier Transformation Fourier Transformation  Fensterfunktionen in der FFT Fensterfunktionen in der FFT |
|||||||||||||||||||||||
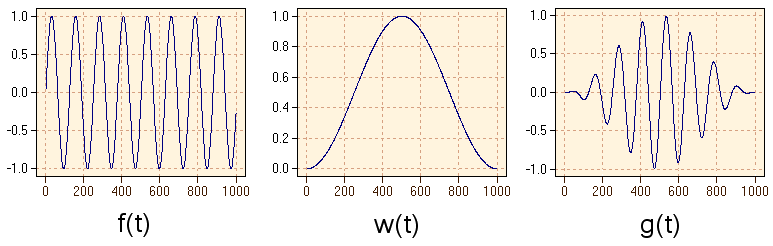
Windowing Function and FFTFFT-based measurements in general suffer from a phenomenon which is called "leackage". By leackage we mean the broadening of the spectral lines and the appearance of side bands if the frequency of the examined oscillation is not an integer multiple of the inverse of the measurement time (which is equivalent to creating a discontinuity at the end of the observed signal when a copy of the signal is appended to it). When calculating the FFT it is implicitely assumed that the signal within the data block (whose length normally is a power of 2) is periodic and the signal is repeated by concatenating copies of the data block infinitely often. This includes that there will be a discontinuity if the signal level and the first derivative at the left and the right end of the data block do not match.
The above mentioned discontinuity results in a broadening of the spectral lines and in the emergence of new spectral lines. In order to suppress this effect one may multiply the measured time series by a weighting function ("windowing function"). If the measured data are not weighted at all, this may be seen equivalent to multiplying the time series by a rectangular function having the width of the measurement window.
If we calculate the Fourier transform of he weighted data, we immediately see that the spectral lines are becoming narrower. The following figure shows the unweighted spetrum at the left and the weighted spectrum at the right:
A multiplication in the original data space is equivalent to a convolution in Fourier space. For example, a multiplication of the original signal with a rectangular function corresponds to the convolution with a sinc function in Fourier space. The selection of a suitable windowing function is always a trade-off between the suppression of side bands and the width of the spectral lines. The following table lists the more important windowing functions:
The cosine bell window, the Hamming window and the general Tukey window are closely related to each other, where the Tukey window is defined as follows: F(x) = 1-2α+2α*cos(x/N)
The parameter α determines the type of the window: Hamming window: α = 0.23The Hanning window in the notation of the Tukey window is equivalent to the cos2 window, which can be easily shown by a few trigonometric transformations.
|
|||||||||||||||||||||||
Home  Bivariate Data Bivariate Data  Time Series Time Series  Fourier Transformation Fourier Transformation  Fensterfunktionen in der FFT Fensterfunktionen in der FFT |
|||||||||||||||||||||||