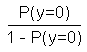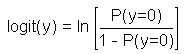Logistic Regression

In the case of a binary reponse variable y one can try to avoid to directly estimate its (binary) values y_i by estimating the probabilities of occurrence, instead. As the response variable is dichotomous it may assume only one out of two possible states (i.e. 0 and 1). If we know the probability of occurrence for one of the states, we automatically also know the probablity of the other state:

P(y=1) = 1 - P(y=0)

The chance for a particular state to occur is thus given by the ratio of the two probabilities:

In order to create a mathematical model one usually uses the logarithm of this chance, which is called "logit":

The logit function transforms the probability of occurrence of a particular state in a way that the 100% certain occurrence of "-1" yields an infinite negative value, the 100% certain occurrence of "+1" results in an infinite positive value. If the odds for both states are equal the logit function returns a zero value.

Starting with the classic regression equation, the response variable y is replaced by the logit function:

logit(y) = a₀ + a₁x₁+ a₂x₂ + a₃x₃ + ....

The main problem with the parametrisation of this logistic regression equation is that the classic least squares approach cannot be used because the possible infinite values of the logit function prohibits its application (due to numeric reasons and due to the leverage effect).

As a consequence the parameter estimation in logistic regression is performed by means of maximum likelihood, which is a generalisation of the least squares method (in the case of normally distributed descriptors the maximum likelihood approach delivers the same results as the least squares regression).