| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Statistical Tests Statistical Tests  Means and Medians Means and Medians  Wilcoxon-Mann-Whitney Test Wilcoxon-Mann-Whitney Test |
|||||||
| See also: [template2_demo.html], Residuals, Wilcoxon Test for Paired Differences, Median Test | |||||||
Wilcoxon-Mann-Whitney TestSometimes t-tests for comparing mean values (more precisely, the t-test for mean value differences) produce results that you don't really trust. In this case, the control with the U-test according to Wilcoxon, Mann and Whitney is suitable.(1) This test can also be used for testing the equality of the mean values in the case of non-normal distributions. The only requirement is that the shape of the distributions of the two samples to be compared is the same (and, strictly speaking, must be continuous).(2)The U-Test checks the following null hypothesis: The probability of an observation drawn from the two populations is for each of the two populations equal (i.e. the distributions are the same):
H0: F1(x) = F2(x) for all x The principle of the U-test is based on the following consideration: If the measured values of the two samples are sorted in a common list in ascending order, the rank sums of the two samples will only differ if, on average, the two samples differ (i.e. one sample shows on average smaller , or larger, values than the other). To calculate the test statistic U, the random samples are marked by their origin (sample 1 or sample 2) and combined and sorted. Next the sum of the rank numbers for sample 1, R1, that for sample 2, R2 are calculated. Then the following applies to the test statistic U:
U1 = n1*n2 + n1(n1+1)/2 - R1 The test statistic U is the smaller of U1 and U2: U = min (U1, U2)
The null hypothesis H0 is rejected if the calculated U-value is less than or equal to the critical value Ukrit (n1, n2, α). Rejecting the null hypothesis means that the distributions are not the same. Since one assumes the same forms of distribution as a prerequisite, it follows that the mean values must be unequal if the null hypothesis is rejected.
|
|||||||
Home  Statistical Tests Statistical Tests  Means and Medians Means and Medians  Wilcoxon-Mann-Whitney Test Wilcoxon-Mann-Whitney Test |
|||||||


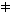 F2(x) for at least one x
F2(x) for at least one x