| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Univariate Data Univariate Data  Distributions Distributions  z-Transform z-Transform |
|||
| See also: Scaling of Data, T-Scores | |||
z-TransformSometimes one has the problem to make two samples comparable, i.e. to compare measured values of a sample with respect to their (relative) position in the distribution. An often used aid is the z-transform which converts the values of a sample into z-scores:
with zi ... z-transformed sample observations The z-transform is also called standardization or auto-scaling. z-Scores become comparable by measuring the observations in multiples of the standard deviation of that sample. The mean of a z-transformed sample is always zero. If the original distribution is a normal one, the z-transformed data belong to a standard normal distribution (μ=0, s=1). The following example demonstrates the effect of the standardization of the data. Assume we have two normal distributions, one with mean of 10.0 and a standard deviation of 30.0 (top left), the other with a mean of 200 and a standard deviation of 20.0 (top right). The standardization of both data sets results in comparable distributions since both z-transformed distributions have a mean of 0.0 and a standard deviation of 1.0 (bottom row).
|
|||
Home  Univariate Data Univariate Data  Distributions Distributions  z-Transform z-Transform |
|||



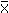 ... sample mean
... sample mean