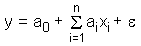| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Multiple Regression Multiple Regression  Einführung Einführung |
|
| Siehe auch: Lineare und nicht lineare Modelle, Regression - Einführung, Variablenauswahl - schrittweise Regression, MLR - Varianzanalyse, Designmatrix, Variance Inflation Factor, Übung - Schätzung von Siedepunkten chemischer Strukturen, Übung - Der Effekt von kollinearen Variablen bei MLR-Modellen, Ridge Regression, MLR und (Multi)Kollinearität, MLR - Selbsttest als multivariater Schätzer, Lineare Diskriminanzanalyse - Einführung | |
| Search the VIAS Library | Index | |
|
Multiple lineare Regression - EinführungAuthor: Hans Lohninger
Die multiple lineare Regression (MLR) ist der einfachen linearen Regression sehr ähnlich. Der einzige Unterschied besteht darin, dass mehr als eine unabhängige Variable zur Modellierung eingesetzt wird. Um den Zusammenhang zwischen n Eingangsvariablen xi und der zu modellierenden Variablen y zu berechnen, können wir die folgende lineare Gleichung verwenden: y = a0 + a1x1 + a2x2 + ... + anxn + ε oder
Der Parameter ε definiert dabei den Fehler oder den Restwert mit einem Mittelwert von null (bei Betrachtung mehrerer y-Werte). Die Gleichung definiert eine Hyperebene im n-dimensionalen Raum. Die Parameter dieser Ebene a0 bis an müssen so angepasst werden, dass die Summe der Fehlerquadrate minimal ist. Die Annahmen sind dieselben wie für die einfache Regression. Die geschätzten Parameter können mit Hilfe einer ANOVA-Tabelle diskutiert werden.
|
|
Home  Multivariate Daten Multivariate Daten  Modellbildung Modellbildung  Multiple Regression Multiple Regression  Einführung Einführung |
|
Last Update: 2012-12-10