Dezimalstellen und Präzision

Author: Hans Lohninger

Ein häufiges Problem bei Berechnungen in der Datenanalyse ist die Verwendung von Werten mit zu vielen Dezimalstellen. Durch den Gebrauch von Taschenrechnern wird dieses Problem noch verstärkt. Besonders Neueinsteiger im Bereich der Datenanalyse sind sich dieses Problems nicht bewusst. Im Allgemeinen sollte man nur so viele Dezimalstellen verwenden, wie mit der Präzision des Experiments vereinbar sind. Es kann deshalb notwendig sein, die Präzision einer Messung durch einige Wiederholungen zu erhöhen und dadurch die Standardabweichung zu verkleinern.

Beispiel:

Nehmen wir an, dass bei einem Experiment mehrere wiederholte Messungen mit folgenden Ergebnissen gemacht wurden: 12.3075 12.3351 11.9949 12.2722 12.3117 12.0766 Die vier Dezimalstellen der Ergebnisse sind bedeutungslos, weil die wiederholten Messungen zeigen, dass höchstens die erste Dezimalstelle stichhaltig ist (eine nähere Analyse zeigt, dass der Mittelwert des Ergebnisses 12.21 ist, mit einer Standardabweichung von 0.14).

Zusätzlich zur eigentlichen Messungenauigkeit kann sich die Genauigkeit von abgeleiteten Größen aber auch noch deutlich verschlechtern, vor allem wenn Differenzen und Quotienten gebildet werden.

Beispiel:

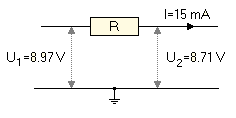Die Berechnung des elektrischen Widerstands nach dem Ohm'schen Gesetz R = U/I. Wir bestimmen dazu den Spannungsabfall U am Widerstand R in dem wir die Spannungen U1 und U2 an beiden Enden messen. Angenommen U1 sei 8.97+/-0.01 V, U2 sei 8.71+/-0.01 V und der Strom I durch den Widerstand wurde mit 0.015+/-0.001 A bestimmt. Aus dem Ohm'schen Gesetz ergibt sich damit folgender Widerstand: R = (8.97-8.71)/0.015 = 17.33 Ohm. Betrachtet man die Messunsicherheiten, so ergeben sich für den errechneten Widerstand folgende Extremwerte: Rmax = (8.98-8.70)/0.014 = 20 Ohm Rmin = (8.96-8.72)/0.016 = 15 Ohm Der Widerstand ist also nur sehr ungenau bestimmt. Es ergibt sich eine Genauigkeit des Widerstandswerts von ca. +/- 15%. Die Angabe des Widerstandswerts ist also nur auf Einerstellen sinnvoll.