| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Univariate Daten Univariate Daten  Lagemaße Lagemaße  Mittelwert Mittelwert  Mittelwert Mittelwert |
||||||||||||||||||||||
| Siehe auch: Median, Modus einer Verteilung, Standardabweichung, Zentraler Grenzwertsatz, Vertrauensbereich des Mittelwerts, Verallgemeinerter Mittelwert, Vergleich von Mittelwerten | ||||||||||||||||||||||
| Search the VIAS Library | Index | ||||||||||||||||||||||
|
MittelwertAuthor: Hans Lohninger
Der Mittelwert wird im allgemeinen Sprachgebrauch als Durchschnitt bezeichnet. Mathematisch gesehen gibt es verschiedene Arten von Mittelwerten, die jeweils in bestimmten Anwendungsszenarien ihre Berechtigung haben:
Hier ein einfaches interaktive Beispiel für eine "naturgetreue" Berechnung des Mittelwerts.
Bedenken Sie bitte, dass es unterschiedliche Notationen für den Mittelwert gibt: Der Mittelwert einer Grundgesamtheit wird mit μ bezeichnet, wohingegen der Mittelwert einer Stichprobe entweder mit m oder mit Der Mittelwert ist eine gute Annäherung an die zentrale Tendenz einer unimodalen symmetrischen Verteilung, kann aber bei schiefen oder multimodalen Verteilungen irreführend sein. Daher ist es hilfreich, bei schiefen Verteilungen zusätzlich andere Lagemaße zu bestimmen (so ist z.B. der Median bei schiefen Verteilungen oder bei Ausreißern deutlich robuster). Eine weitere Möglichkeit mit Ausreißern umzugehen, ist die Benutzung eines getrimmten Mittelwerts, den man ermittelt in dem man die kleinsten und größten Werte vor der Berechnung des Mittelwerts entfernt (typischerweise werden 5% der Werte weggelassen).
|
||||||||||||||||||||||
Home  Univariate Daten Univariate Daten  Lagemaße Lagemaße  Mittelwert Mittelwert  Mittelwert Mittelwert |
||||||||||||||||||||||
Last Update: 2021-08-15


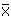 dann zu:
dann zu: