Lineare Diskriminanzanalyse - Einführung

Author: Hans Lohninger

Die lineare Diskriminanzanalyse (engl. linear discriminant analysis, LDA) ist eine Methode, mit der man zwischen zwei oder mehr Stichprobengruppen unterscheiden kann. Um einen Klassifikator basierend auf LDA zu entwickeln, müssen folgende Schritte durchgeführt werden:

Festlegung der Gruppen

Festlegung der Diskriminanzfunktion

Abschätzung der Diskriminanzfunktion

Testen der Diskriminanzfunktion

Anwendung

Festlegung der Gruppen:

Die zu unterscheidenden Gruppen können sich entweder aus dem untersuchten Problem oder durch vorangehende Analysen, wie z.B. der Clusteranalyse, ergeben. Die Anzahl der Gruppen ist nicht notwendigerweise auf zwei beschränkt, obwohl die Unterscheidung zwischen zwei Gruppen die üblichste Methode ist. Beachten Sie, dass die Zahl der Gruppen die Zahl der Variablen nicht überschreiten darf. Eine weitere Voraussetzung ist, dass die Gruppen dieselbe Kovarianzstruktur haben (d.h. sie müssen vergleichbar sein).

Festlegung der Diskriminanzfunktion:

Im Prinzip kann jede mathematische Funktion als Diskriminanzfunktion verwendet werden. Im Falle der LDA wird eine lineare Funktion der Form

mit x_i als beschreibende Variablen verwendet. Die Parameter a_i müssen so bestimmt werden, dass die Trennung der Gruppen optimal ist. Beachten Sie, dass die lineare Diskriminanzfunktion formal der multiplen linearen Regression gleicht. Tatsächlich kann man direkt die MLR anwenden, wenn die abhängige Variable y durch die gewichteten Klassenzahlen c₁ und c₂ ersetzt wird.

c₁ = n₂/(n₁+n₂) und c₂ = - n₁/(n₁+n₂)

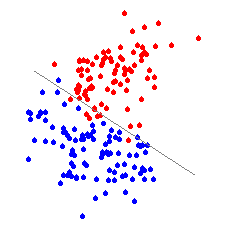
Um ein besseres Verständnis für die Wirkungsweise der Diskriminanzfunktion zu bekommen, sollten Sie dieses interaktive Beispiel starten.

Abschätzung der Parameter der Diskriminanzfunktion:

Wie Sie im interaktiven Beispiel sehen konnten, gibt es nur eine Richtung der Diskriminanzfunktion, die die besten Trennungsergebnisse liefert. Die Bestimmung der Koeffizienten der Diskriminanzfunktion ist sehr einfach. Im Prinzip wird die Diskriminanzfunktion so gebildet, dass die Trennung (= Entfernung) zwischen den Gruppen maximal und die Entfernung innerhalb der Gruppen minimal ist.

Testen der Diskriminanzfunktion:

Nachdem die Diskriminanzfunktion mit Parametern versehen wurde, muss sie entweder durch einen unabhängigen Satz von Testdaten oder durch Kreuzvalidierung getestet werden. In beiden Fällen sollte das Testergebnis mit den Trainingsdaten vergleichbar sein.

Anwendung:

Die Diskriminanzanalyse kann entweder zur Analyse oder zur Klassifikation verwendet werden:

• Analyse: Wie kann das Material interpretiert werden? Welche Variablen tragen am meisten zum Unterschied bei?
• Klassifikation: Angenommen eine Diskriminanzfunktion kann gefunden werden, die eine zufriedenstellende Trennung ergibt, so kann diese Funktion für die Klassifizierung von Daten eingesetzt werden.