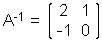| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Mathematischer Hintergrund Mathematischer Hintergrund  Matrizen Matrizen  Lineare Gleichungen Lineare Gleichungen  Äquivalenzoperationen Äquivalenzoperationen |
|||
| Siehe auch: Gauß-Jordan-Algorithmus, Lineare Gleichungssysteme | |||
| Search the VIAS Library | Index | |||
|
ÄquivalenzoperationenAuthor: Hans Lohninger
Ein Schlüssel, um lineare Gleichungen zu lösen, sind Äquivalenzoperationen, die ein System aus linearen Gleichungen verändern, ohne die Lösung zu verändern. Zum Verständnis der folgenden Abschnitte, sollten Sie sich erinnern, dass Systeme von linearen Gleichungen als Matrizen dargestellt werden können.
Für andere Zwecke können Sie Reihenoperationen durch Spaltenoperationen ersetzen, was zum gleichen Ergebnis führt, obwohl sie die Lösungen eines Systems von linearen Gleichungen nicht erhalten. Beispiel: Manuelle Berechnung der Inversen einer Matrix Ein Beispiel, wie man den Vorteil von Reihen- oder Spalten-Äquivalenzoperationen verwenden kann, ist die manuelle Berechnung einer Inversen. Lassen Sie uns die Inverse von
Nun werden wir Äquivalenzoperationen anwenden, um den grünen Teil der erweiterten Matrix in eine Einheitsmatrix zu transformieren. Das wird in der inversen Matrix A-1 resultieren, die in der roten Submatrix enthalten ist. Wir starten, indem wir beide Reihen vertauschen (Regel 1, siehe oben).
Als Nächstes addieren wird die zweite Reihe zweimal zu der ersten (Regel 2, siehe oben) und erhalten:
Nachdem wir die zweite Reihe mit -1 (Regel 3, siehe oben) multipliziert
haben, verbleiben wir mit:
Also haben wir schließlich A-1 berechnet:
|
|||
Home  Mathematischer Hintergrund Mathematischer Hintergrund  Matrizen Matrizen  Lineare Gleichungen Lineare Gleichungen  Äquivalenzoperationen Äquivalenzoperationen |
|||
Last Update: 2012-10-08