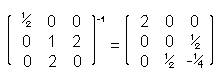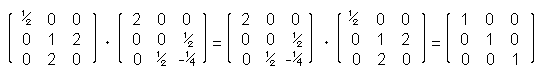Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu.

Home Mathematischer Hintergrund Matrizen Inverse Matrizen Inversion von Matrizen
Siehe auch: Einheitsmatrix, Moore-Penrose pseudo-inverse Matrix, Stochastische und reguläre Matrix, Eigenvektoren und Eigenwerte 
 
Search the VIAS Library  |  Index


Inversion von Matrizen

Author: Hans Lohninger

Die Inversion von Matrizen spielt bei multivariaten Methoden eine bedeutende Rolle. Während die Inverse einer Matrix nur für quadratische Matrizen definiert ist, kann das Konzept der Matrixinversion durch Pseudo-Inversion auch auf rechteckige Matrizen ausgeweitet werden.

Inverse Matrix Für eine quadratische Matrix A ist die inverse Matrix X durch folgende Gleichung definiert:
AX = I
Die Inverse von A wird als A-1 geschrieben und ist eindeutig. Beachten Sie, dass nicht alle quadratischen Matrizen invertierbar sind. Falls eine Inverse zu A existiert, wird A als reguläre oder nicht-singuläre Matrix bezeichnet. Im anderen Fall ist A eine singuläre Matrix. Für reguläre Matrizen ist folgende Gleichung gültig: A A-1 = A -1A = I.

Die Inverse einer Matrix kann mit Hilfe verschiedener Algorithmen berechnet werden; einer davon ist das Gauß-Jordan-Verfahren.

Rechenregeln:

(A-1) -1 = A

(A-1) T = (AT) -1

(AB)-1 = B-1A -1

(λA)-1 = λ-1A -1

Beispiel:

da

Home Mathematischer Hintergrund Matrizen Inverse Matrizen Inversion von Matrizen

Last Update: 2012-10-08