Geometrische Bedeutung der Matrixmultiplikation

Author: Hans Lohninger

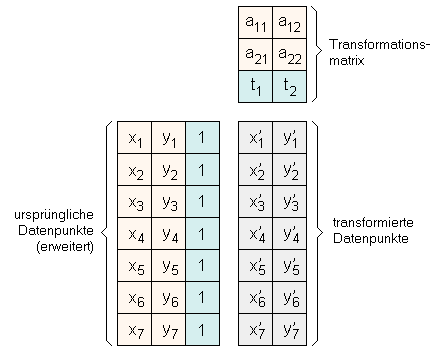
Die Matrizenmultiplikation ist ein vielseitiges Werkzeug für viele wissenschaftliche oder technische Methoden. Eine spezielle Anwendung der Matrizenmultiplikation ist die Transformation von Daten im n-dimensionalen Raum. Die Daten können durch eine simple Matrizenmultiplikation skaliert, verschoben, rotiert oder verdreht werden. Um alle diese Operationen durch eine einzige Matrixtransformation auszuführen, muss die Originaldatenmatrix durch einen zusätzlichen konstanten Wert (vorzugsweise 1) erweitert werden. Die Effekte der Matrizenmultiplikation können Sie durch das folgende interaktive Beispiel sehen.

Beispiel: Transformation von zweidimensionalen Punkten. Nehmen wir an, wir hätten 7 Datenpunkte in 2 Dimensionen (x und y). Diese 7 Datenpunkte müssen verschiedensten Transformationsoperationen unterzogen werden. Dafür erweitern wir die Datenmatrix, geschrieben als [x_i,y_i], mit einem konstanten Wert von 1, was in den Punktvektoren [x_i,y_i,1] resultiert.

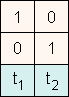
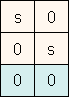
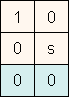
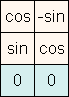
Um die verschiedenen Transformationen auszuführen, müssen wir einfach die Transformationsmatrix entsprechend anpassen.

Verschiebung		Die Koordinaten der Datenpunkte werden durch den Vektor [t1,t2] verschoben.
Skalierung		Die Punkte werden mit dem Faktor s skaliert.
Skalieren der y-Koordinate		Hier werden nur die y-Koordinaten anhand des Faktors s skaliert.
Rotation		Eine Rotation aller Punkte um den Ursprung. Dies kann durch Anwendung der Sinus- bzw. Kosinusfunktion des Rotationswinkels bewerkstelligt werden.