Addition von Rauschen

Author: Hans Lohninger

Generalisierung ist ein sehr wichtiger Aspekt bei der Erstellung von nicht linearen Modellen (besonders, wenn neuronale Netzwerke eingesetzt werden). Um gut arbeitende Modelle zu erstellen, muss man die Verallgemeinerungsfähigkeit des Modells überprüfen. In dieser Hinsicht kann Verallgemeinerung als Rauschunempfindlichkeit gesehen werden: Das Modell sollte sich selbst nicht an vorhandenes Rauschen im System anpassen. Dieser Aspekt bringt uns auf den Gedanken, dass das Verallgemeinerungsverhalten eines Modells durch die steigende Zugabe von Rauschen zu den Trainingsdaten - bei gleichzeitiger Überprüfung der Stabilität des Modells - getestet werden kann.

Um den Verallgemeinerungstest durchführen zu können, benötigen wir zwei Maße:

• Das Bestimmtheitsmaß der Modellschätzung (Quadrate des Korrelationskoeffizienten zwischen Stichprobe und geschätzten Daten): r²_t,e
• Das Quadrat des Korrelationskoeffizienten zwischen den geschätzten Daten des originalen Datensatzes und den geschätzten Daten, berechnet aus den verrauschten Daten: r²_e0,en

Diese Werte werden bei verschiedenen Rauschpegeln berechnet. Die Trends der zwei Werte bei Erhöhung des Rauschpegels deuten die Verallgemeinerungsfähigkeit des Netzwerks an. Ein gut arbeitendes Netzwerk zeigt ein sinkendes r²_t,e, da der steigende Rauschpegel nicht in der geschätzten Funktion widergespiegelt wird. Auf der anderen Seite sollte der Wert von r²_e0,en möglichst konstant bleiben, da sich die geschätzte Funktion eines verrauschten Datensatzes kaum von der geschätzten Funktion des originalen Datensatzes unterscheidet. Bei Überanpassung (also schlechter Generalisierung) ist die Lage genau umgekehrt: Der Parameter r²_t,e ist fast konstant und der Wert von r²_e0,en nimmt mit steigendem Rauschen ab, da die Netzwerke dazu tendieren, sich an die verrauschten Daten anzupassen und den dahinter liegenden Trend der Daten vernachlässigen.

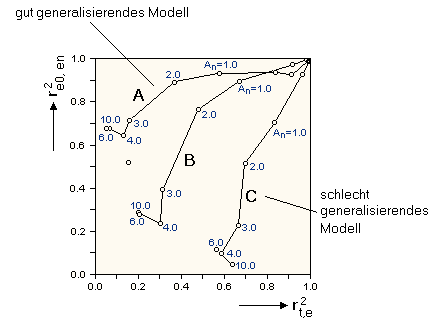
In der Abbildung oben wird die Abhängigkeit von r²_t,e und r²_e0,en von verschiedenen Rauschpegeln A_n für drei unterschiedliche Netze gezeigt. Kurve A (gute Verallgemeinerung): 400 Datenpunkte, 15 verdeckte Neuronen; Kurve B (mittlere Verallgemeinerung): 200 Datenpunkte, 38 verdeckte Neuronen; Kurve C (schlechte Verallgemeinerung): 100 Datenpunkte, 70 verdeckte Neuronen.