| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Mathematischer Hintergrund Mathematischer Hintergrund  Wahrscheinlichkeit Wahrscheinlichkeit  Bayes'sches Gesetz Bayes'sches Gesetz |
|||||||||||||||
| Siehe auch: Bedingte Wahrscheinlichkeit, Selektivität und Spezifität | |||||||||||||||
| Search the VIAS Library | Index | |||||||||||||||
|
Bayes'sches GesetzAuthor: Hans Lohninger
In manchen Situationen ist es einfacher die Wahrscheinlichkeit eines Ereignisses zu berechnen, wenn man weiß, dass auch ein anderes Ereignis eingetreten ist. Das Bayes'sche Gesetz ermöglicht es, die Wahrscheinlichkeit eines Ereignisses zu berechnen, indem vorher bestimmt wird, ob andere Ereignisse eingetreten sind oder nicht. Mit den gegebenen Ereignissen A und B können wir A auch als A = (A
Weil (A P(A) = P (A Die Wahrscheinlichkeit des Ereignisses A ist der gewichtete Mittelwert der bedingten Wahrscheinlichkeiten von A, wenn B gegeben ist, und A, wenn B nicht gegeben ist. Die Gewichte der bedingten Wahrscheinlichkeiten sind durch die Wahrscheinlichkeiten der bedingten Ereignisse B und B' (nicht B) definiert. Bayes'sche Formel: Das Gesetz, oben für die Ereignisse A und B entwickelt, kann auch für mehr als zwei Ereignisse verallgemeinert werden. Falls der Probenraum aus n einander ausschließenden Ereignissen Fi besteht, ist die Wahrscheinlichkeit für das Ereignis E:  P(E) ist der gewichtete Mittelwert von P(E|Fi); das Gewicht ist die Wahrscheinlichkeit des Ereignisses Fi, auf das E beschränkt ist.
Wenn wir Fj als Hypothesen über eine Frage interpretieren, zeigt uns die Bayes'sche Formel, wie der Beweis unsere Meinung, die wir vorher über das Experiment gehabt haben, verändern sollte.
|
|||||||||||||||
Home  Mathematischer Hintergrund Mathematischer Hintergrund  Wahrscheinlichkeit Wahrscheinlichkeit  Bayes'sches Gesetz Bayes'sches Gesetz |
|||||||||||||||
Last Update: 2012-10-08


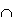 B)
B) 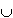 (A
(A