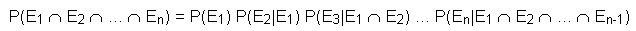|
Unabhängige Ereignisse
Author: Hans Lohninger
A und B sind voneinander unabhängige Ereignisse, wenn
das Auftreten von B die Wahrscheinlichkeit, dass A eintritt, nicht beeinflusst
(und umgekehrt):
P(A|B) = P(A)
und
P(B|A) = P(B).
Experimente werden normalerweise so geplant, dass sie unabhängig sind.
| Beispiel: |
Eine Münze wird zwei Mal geworfen. Wir definieren die
Ereignisse A als "der erste Wurf ist Kopf" und B als "der zweite Wurf ist
Kopf". Beeinflusst der erste Wurf das Ergebnis des zweiten Wurfs? Ganz
intuitiv würden wir "Nein" sagen, aber wir wollen es beweisen:
P(A) = P(HH) + P(HT) = ½ ,
P(B) = P(TH) + P(HH) = ½.
P(B|A) = P(A 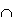 B) / P(A) = P(HH) / P(A) = ¼ / ½ = ½ B) / P(A) = P(HH) / P(A) = ¼ / ½ = ½
Wir sehen also, dass P(B|A) = P(B) ist, daraus folgt,
dass das Ereignis A keinen Einfluss auf das Ergebnis von B hat. Die Ereignisse
sind voneinander unabhängig. |
ANMERKUNG
- "Unabhängigkeit" ist ein schwieriges Konzept und kann nicht in einem
Diagramm dargestellt werden. Unabhängigkeit ist nicht intuitiv und man muss
sie für jede Situation überprüfen.
- Die Wahrscheinlichkeit der Schnittmenge von unabhängigen Ereignissen ist
das Produkt der Wahrscheinlichkeiten der Ereignisse: P(A
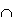 B) = P(A) . P(B) B) = P(A) . P(B)
Das kann aus der Gleichung P(A 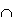 B) = P(A) . P(B|A) abgeleitet werden, wobei P(B|A) =
P(B), wenn die Ereignisse unabhängig sind. B) = P(A) . P(B|A) abgeleitet werden, wobei P(B|A) =
P(B), wenn die Ereignisse unabhängig sind.
- Wenn A und B unabhängig sind, dann sind A und B' auch unabhängig.
- Zwei einander ausschließende Ereignisse A und B sind immer unabhängig!
Wenn B eingetreten ist, ist es für A unmöglich, simultan aufzutreten.
- Wenn A unabhängig von B und A unabhängig von C ist, muss A nicht
notwendigerweise auch von (B
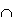 C) unabhängig sein. C) unabhängig sein.
Unabhängigkeit von mehreren Ereignissen
Wenn 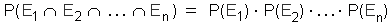 , dann sind auch alle Subereignisse Ei unabhängig. Eine Menge von Ereignissen ist
unabhängig, wenn jede endliche Untermenge dieser Ereignisse auch unabhängig ist.
Manchmal besteht die Wahrscheinlichkeit eines Experiments aus einer Reihe von
Unterexperimenten (ein Wurf beim mehrmaligen Werfen von Münzen). In vielen
Fällen können wir annehmen, dass die Ergebnisse unabhängig sind. Wenn alle
Experimente identisch sind und denselben Probenraum und dieselbe
Wahrscheinlichkeit haben, gilt: , dann sind auch alle Subereignisse Ei unabhängig. Eine Menge von Ereignissen ist
unabhängig, wenn jede endliche Untermenge dieser Ereignisse auch unabhängig ist.
Manchmal besteht die Wahrscheinlichkeit eines Experiments aus einer Reihe von
Unterexperimenten (ein Wurf beim mehrmaligen Werfen von Münzen). In vielen
Fällen können wir annehmen, dass die Ergebnisse unabhängig sind. Wenn alle
Experimente identisch sind und denselben Probenraum und dieselbe
Wahrscheinlichkeit haben, gilt:
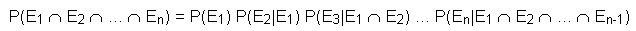
|


 Mathematischer Hintergrund
Mathematischer Hintergrund  Wahrscheinlichkeit
Wahrscheinlichkeit  Unabhängige Ereignisse
Unabhängige Ereignisse Mathematischer Hintergrund
Mathematischer Hintergrund  Wahrscheinlichkeit
Wahrscheinlichkeit  Unabhängige Ereignisse
Unabhängige Ereignisse

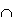 B) / P(A) = P(HH) / P(A) = ¼ / ½ = ½
B) / P(A) = P(HH) / P(A) = ¼ / ½ = ½
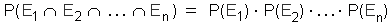 , dann sind auch alle Subereignisse Ei unabhängig. Eine Menge von Ereignissen ist
unabhängig, wenn jede endliche Untermenge dieser Ereignisse auch unabhängig ist.
Manchmal besteht die Wahrscheinlichkeit eines Experiments aus einer Reihe von
Unterexperimenten (ein Wurf beim mehrmaligen Werfen von Münzen). In vielen
Fällen können wir annehmen, dass die Ergebnisse unabhängig sind. Wenn alle
Experimente identisch sind und denselben Probenraum und dieselbe
Wahrscheinlichkeit haben, gilt:
, dann sind auch alle Subereignisse Ei unabhängig. Eine Menge von Ereignissen ist
unabhängig, wenn jede endliche Untermenge dieser Ereignisse auch unabhängig ist.
Manchmal besteht die Wahrscheinlichkeit eines Experiments aus einer Reihe von
Unterexperimenten (ein Wurf beim mehrmaligen Werfen von Münzen). In vielen
Fällen können wir annehmen, dass die Ergebnisse unabhängig sind. Wenn alle
Experimente identisch sind und denselben Probenraum und dieselbe
Wahrscheinlichkeit haben, gilt: