| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Mathematischer Hintergrund Mathematischer Hintergrund  Wahrscheinlichkeit Wahrscheinlichkeit  Wichtige Regeln Wichtige Regeln |
|
| Siehe auch: Ereignisse und Stichprobenraum | |
| Search the VIAS Library | Index | |
|
Wichtige RegelnAuthor: Hans Lohninger
Wenn man Elemente aus einer Menge auswählt, hängt die Anzahl an möglichen Ergebnissen von den Bedingungen, unter denen die Selektion stattgefunden hat, ab. Es gibt zumindest vier Regeln, um die Anzahl der möglichen Ergebnisse zu zählen: MultiplikationsgesetzStellen Sie sich vor, Sie haben j Mengen von Elementen, n1 in der ersten Menge, n2 in der zweiten Menge ... und nj in der j-ten Menge. Sie möchten nun eine Probe von j Elementen formen, indem Sie jeweils ein Element aus jeder der j Mengen nehmen. Die Anzahl an möglichen Mengen ist durch n1 definiert.
PermutationsgesetzDie Anordnung von Elementen in einer unverkennbaren Reihenfolge wird Permutation genannt. Aus einer gegebenen Menge von n unverwechselbaren Elementen, möchten Sie k Elemente aus den n auswählen und sie auf k Positionen anordnen. Die Anzahl der verschiedenen Permutationen der n Elemente, wenn k auf einmal gezogen wurden, wird als Pkn geschrieben und entspricht:
.
PartitionsgesetzNehmen wir an, eine einzelne Menge von n unverwechselbaren Elementen existiert. Sie möchten sie auf k Mengen aufteilen, wobei die erste Menge n1 Elemente, die zweite n2 Elemente ... und die k-te nk Elemente enthalten soll. Die Anzahl an verschiedenen Aufteilungen ist dann
wobei n1 + n2 + ...+ nk =n. Der Zähler spiegelt die Permutationen der n Elemente wider, der Nenner reduziert diese Permutationen um die Duplikate in den k Untermengen.
KombinationsgesetzEine Stichprobe von k Elementen soll aus einer Menge von n Elementen ausgewählt werden. Die Anzahl der verschiedenen Stichproben aus k Elementen, die aus n gewählt werden können, entspricht: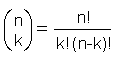 . .Das Kombinationsgesetz ist eine spezielle Anwendung des Partitionsgesetzes, mit j = 2 und n1= k. Aus n = n1+ n2 folgt, dass n2 durch (n - n1) ersetzt werden kann. Normalerweise verweisen die zwei Gruppen auf die zwei verschiedenen Gruppen der gewählten und nicht gewählten Proben. Die Reihenfolge in der die n1 Elemente gezogen werden, ist nicht wichtig, deshalb gibt es weniger Kombinationen als Permutationen (Binomialtheorem).
Bemerkung: Die Faktorielle n! ist durch n! = 1  2 2  3 3  ...(n-2)
...(n-2)  (n-1) (n-1)  n definiert. (0! ist als 1 definiert.) n definiert. (0! ist als 1 definiert.)
|
|
Home  Mathematischer Hintergrund Mathematischer Hintergrund  Wahrscheinlichkeit Wahrscheinlichkeit  Wichtige Regeln Wichtige Regeln |
|
Last Update: 2012-10-08



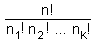 ,
,