| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Bivariate Daten Bivariate Daten  Regression Regression  Konfidenzintervall Konfidenzintervall |
|||||||
| Siehe auch: Regression - Gerade, Ableitung einer Regressionsformel, Vertrauensbereich | |||||||
| Search the VIAS Library | Index | |||||||
|
Regression - KonfidenzintervallAuthor: Hans Lohninger
mit
Wenn man das Konfidenzintervall für die Regressionsgerade grafisch
darstellt, erkennt man, dass diese Linien hyperbolisch sind. Das bedeutet, dass
das Konfidenzintervall vom X-Wert abhängig ist. Je weiter sich der X-Wert
von
In der Praxis wird das Konfidenzintervall für die Grundgesamtheit nicht oder nur selten benötigt, da die meisten Schlussfolgerungen auf der Schätzung eines bestimmten, zukünftigen
mit
Das Konfidenzintervall für konkrete (zukünftige) Werte von Y ist breiter als das Konfidenzintervall für den Mittelwert der Grundgesamtheit (äußere graue Kurve im Diagramm oben). Der Schätzwert für einen konkreten Y-Wert ist also weniger genau als der Schätzwert des Mittelwertes von Y.
|
|||||||
Home  Bivariate Daten Bivariate Daten  Regression Regression  Konfidenzintervall Konfidenzintervall |
|||||||
Last Update: 2020-11-05



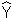 i bei jedem Wert der
unabhängigen Variablen X. Dieser geschätzte Mittelwert ist normal verteilt.
Nun kann man nach dem
i bei jedem Wert der
unabhängigen Variablen X. Dieser geschätzte Mittelwert ist normal verteilt.
Nun kann man nach dem  s2
t1-α;n-2
s2
t1-α;n-2


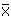 entfernt, desto größer ist das Konfidenzintervall (innere blaue Kurve im Diagramm unten). Das Band das durch das Konfidenzintervall für alle X-Werte gebildet wird, wird auch Working-Hotelling Konfidenzband genannt.
entfernt, desto größer ist das Konfidenzintervall (innere blaue Kurve im Diagramm unten). Das Band das durch das Konfidenzintervall für alle X-Werte gebildet wird, wird auch Working-Hotelling Konfidenzband genannt.

