| Grundlagen der Statistik enthält Materialien verschiedener Vorlesungen und Kurse von H. Lohninger zur Statistik, Datenanalyse und Chemometrie .....mehr dazu. |

|

Home  Allgemeine Bearbeitungsschritte Allgemeine Bearbeitungsschritte  Datenerfassung Datenerfassung  Abtasttheorem Abtasttheorem |
|||
| Search the VIAS Library | Index | |||
|
AbtasttheoremAuthor: Hans Lohninger
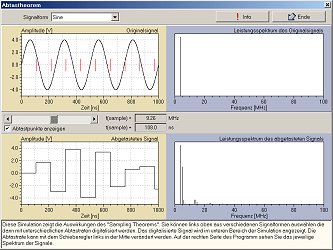
Die zentrale Frage bei der digitalen Erfassung eines Messsignals ist folgende: Kann ich aus dem digitalisierten Messsignal das Originalsignal wieder herstellen oder nicht? Oder anders gefragt: Wie groß muss die minimale Abtastfrequenz sein, damit ich das Originalsignal aus den digitalen Werten wieder rekonstruieren kann? Man könnte dieser Frage aus dem Weg gehen, in dem man das Messsignal mit einer extrem hohen Abtastrate abtastet (z.B. 109 Samples/Sekunde). Allerdings führt das letztendlich in kurzer Zeit zu nicht mehr handhabbaren Datenmengen; außerdem sind solche Messanordnungen viel zu teuer für die tägliche Praxis. Als logische Konsequenz muss die Abtastrate gesenkt werden, und zwar möglichst so weit, dass trotz einer niedrigen Abtastrate das Originalsignal nicht verfälscht wird.
Die Antwort auf diese Frage wurde bereits 1928 von Harry Nyquist gegeben, allerdings erfolgte der formale Beweis erst 1949 durch Claude E. Shannon. Die zentrale Aussage dieser beiden Arbeiten wird heute allgemein als das Abtasttheorem bezeichnet. Das Abtasttheorem besagt, dass die Abtastfrequenz mindesten 2 mal so hoch sein muss wie die Bandbreite BW des Messsignals: fs > 2*BW Manchmal wird anstatt der Bandbreite auch die höchste im Signal vorkommende Frequenz verwendet.Die Frage, die sich automatisch stellt ist nun: Wie kann ich die Bandbreite des Signals erkennen? Dazu führt man eine Fouriertransformation des Messsignals durch, so dass man aus dem Spektrum des Signals dessen Bandbreite ablesen kann. Für die Praxis stellt sich die Frage aus etwas anderer Sicht: Wie kann man sicher sein, dass das Abtasttheorem erfüllt ist? Um die Randbedingungen des Abtasttheorems zu erfüllen, gibt es zwei Möglichkeiten: (1) das Signal bandbegrenzen auf die halbe Abtastfrequenz (Achtung - jede Bandbegrenzung vernichtet Information!) (2) Die Abtastfrequenz entsprechend erhöhen. Im Allgemeinen wird man aber das zu messende Signal ohnehin so genau kennen, dass man die passende Abtastfrequenz relativ leicht und mit wenig Aufwand abschätzen kann (so verlangt z.B. eine Messung der Raumtemperatur natürlich nur eine geringe Abtastrate, da sich die Temperatur ja nur sehr langsam ändert). Was passiert, wenn das Abtasttheorem nicht erfüllt ist? In diesem Fall entspricht das aus den digitalen Werten rekonstruierte Signal nicht mehr dem Originalsignal. Der entstehende Artefakt kann ein Signal vorgaukeln, dass es im Original gar nicht gibt. Ein einfaches Experiment soll die Verhältnisse klären helfen. Angenommen wir müssen ein Signal erfassen, das einen sinusförmigen Verlauf aufweist. Nach der Digitalisierung werden die Werte mit Hilfe eines DA-Wandlers wieder in ein analoges Signal umgeformt. Je nach Abtastrate ergibt sich dadurch eine Kurvenform die um so eher dem Originalsignal entspricht, je höher die Abtastrate liegt. In der Abbildung links ist oben ein Sinussignal mit einer Frequenz von 4 MHz dargestellt. Darunter sind die digitaliserten Verläufe bei unterschiedlichen Abtastraten abgebildet. Wie man aus dieser Abbildung leicht erkennen kann, zumindest die Frequenz des Sinussignals erst bei einer Abtastrate von 10 MHz korrekt bestimmbar; bei 5 MHz Abtastrate hat das entstehende Signal überhaupt nichts mehr mit dem Original zu tun. Erst bei sehr hohen Abtastraten (160 MHz, ganz unten) wird das Sinussignal als solches erkennbar. Normalerweise wird man nach der DA-Wandlung ein Tiefpassfilter einbauen, dessen Grenzfrequenz der halben Abtastfrequenz entspricht. Durch dieses Tiefpassfilter werden die Stufen "geglättet" und es entsteht wieder das Originalsignal.
Vergleich der Amplituden- und der Zeitauflösung: Um ein Signal möglichst fehlerfrei zu digitalisieren, müssen sowohl die Zeitauflösung als auch die Amplitudenauflösung bestimmten Kriterien genügen. Die zeitliche Auflösung ergibt sich aus der Abtastfrequenz, die ihrerseits durch das Abtasttheorem kontolliert wird. Die Amplitudenauflösung des AD-Wandlers stellt eine Obergrenze der maximal möglichen Genauigkeit der Datenerfassung dar.
|
|||
Home  Allgemeine Bearbeitungsschritte Allgemeine Bearbeitungsschritte  Datenerfassung Datenerfassung  Abtasttheorem Abtasttheorem |
|||
Last Update: 2012-10-08