| Fundamentals of Statistics contains material of various lectures and courses of H. Lohninger on statistics, data analysis and chemometrics......click here for more. |

|

Home  Bivariate Data Bivariate Data  Correlation Correlation  Covariance Covariance |
|
| See also: correlation coefficient | |
Covariance
Assume you have two variables which are related to each other to some extent. In order to define a measure for the relationship between x any y we may try to sum up the products of the x and y coordinates for all data points. Inspecting this measure more closely, however, reveals that this number is heavily dependant on the absolute values of the coordinates. If we add a constant amount to all coordinates (which means shifting the data in the x-y-plane without changing their mutual relationship), our measure will increase approximately by the square of the added value. So what we need is a value which is independent of any shifting along the axes (invariance of translation). In order to achieve this, we subtract the mean of the x and the y data before calculating the average of the product terms:
This measure is known as the covariance, and is independent of any translations. The covariance plays an important role in multivariate statistics. Hint: When checking the covariance for independence
of scaling we discover that it is not independent. We therefore have to
refine the definition of the covariance in order to achieve independence
of scaling (invariance of scaling). The resulting measure is known
as the correlation coefficient.
|
|
Home  Bivariate Data Bivariate Data  Correlation Correlation  Covariance Covariance |
|


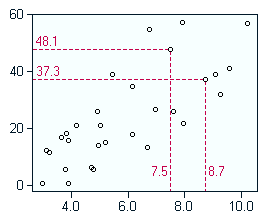 There
are several measures to describe the relationship between two variables,
one of these descriptors being the covariance, another one the
There
are several measures to describe the relationship between two variables,
one of these descriptors being the covariance, another one the