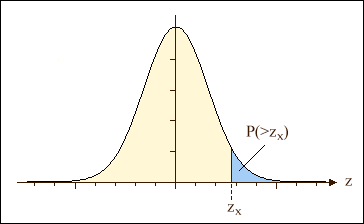
Level of Significance

When observing a random process, there is always a certain probability that the results are above some threshold. The probability of this threshold being exceeded is called the level of significance α. Statisticians usually say "statistically significant at the 5% level", which means that there is 5% chance that the observed value occurs at random.⁽¹⁾ This term originates from the theory of statistical tests, where the random process is the test statistic. If the test statistic exceeds the limit z_x (the critical threshold), the probability of making a type I error is α.

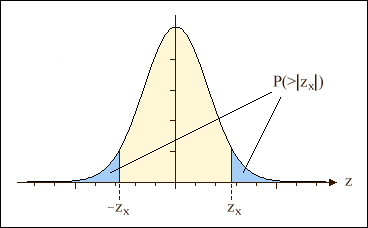
The shaded area of the distribution density above specifies the probability that the outcome z of an experiment exceeds the threshold value z_x. Please note that in some cases, the interesting question may implicitly refer to two thresholds, as shown below:

In this case, the level of significance is the sum of the areas below -z_x and above +z_x.

(1)	In scientific publications you may find terms such as "highly significant", or "insignificant". These terms always refer to the level of significance of a test. There's common concent about the wording: α > 0.05 (> 5%) .... insignificant α = 0.01 to 0.05 (1 to 5%) .... significant α = 0.001 to 0.01 (0.1 to 1%) .... highly significant α ≤ 0.001 (≤ 0.1%) .... conclusive (very highly significant)